Question

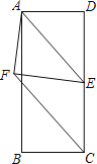
【题目】 如图，在矩形ABCD中，AB=8，AD=3，点E是CD的中点，连接AE，将△ADE沿直线AE折叠，使点D落在点F处，则线段CF的长度是______．

Answer 1

【答案】

【解析】

由折叠可得全等形，由中点、勾股定理可求出AE的长，得到三角形EFC是等腰三角形，利用三线合一和勾股定理使问题得以解决．

解：过点E作EG⊥FC垂足为G，

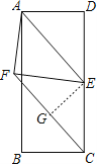
∵点E是CD的中点，矩形ABCD中，AB=8，AD=3，

∴DE=EC=4，

在Rt△ADE中，AE==5，

由折叠得：∠DEA=∠AEF，DE=EF=DC=4，

又∵EG⊥FC

∴∠FEG=∠GEC，FG=GC，

∴∠AEG=×180°=90°，

∴△ADE∽△EGC，

∴即：，

解得：CG=，

∴FC=，

故答案为：．