题目内容
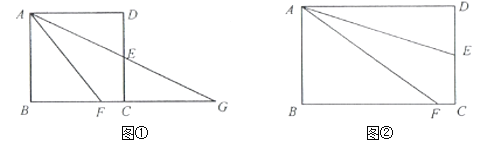
【题目】如图,将矩形ABCD绕点A顺时针旋转θ(0°≤θ≤360°),得到矩形AEFG.
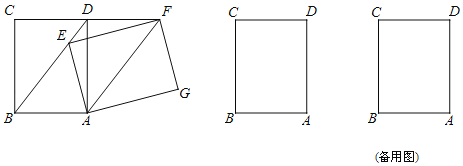
(1)当点E在BD上时,求证:AF∥BD;
(2)当GC=GB时,求θ;
(3)当AB=10,BG=BC=13时,求点G到直线CD的距离.
【答案】(1)见解析;(2)60°或300°;(3)25或1
【解析】
(1)先运用SAS判定△FEA≌△DAB,可得∠AFE=∠ADE=∠DEF,即可得出AF∥BD;
(2)当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论,依据∠DAG=60°,即可得到旋转角θ的度数.
(3)当BG=BC时存在两种情况:画图根据勾股定理计算即可.
(1)由旋转可得,AE=AB,∠AEF=∠DAB=90°,EF=BC=AD,
∴∠AEB=∠ABE,△FEA≌△DAB(SAS),
∴∠AFE=∠ADB,
又∵∠ABE+∠EDA=90°=∠AEB+∠DEF,
∴∠EDA=∠DEF,
∴∠DEF=∠AFE,
∴AF∥BD;
(2)如图1,当GB=GC时,点G在BC的垂直平分线上,分两种情况讨论:
①当点G在AD右侧时,取BC的中点H,连接GH交AD于M,连接DG,
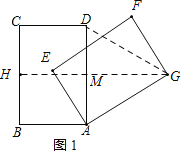
∵GC=GB,
∴GH⊥BC,
∴四边形ABHM是矩形,
∴AM=BH=![]() AD=
AD=![]() AG,
AG,
∴GM垂直平分AD,
∴GD=GA=DA,
∴△ADG是等边三角形,
∴∠DAG=60°,
∴旋转角θ=60°;
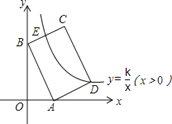
②当点G在AD左侧时,如图2,同理可得△ADG是等边三角形,
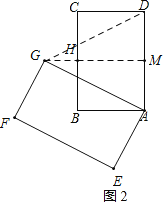
∴∠DAG=60°,
∴旋转角θ=360°﹣60°=300°.
综上,θ的度数为60°或300°;
(3)有两种情况:
①如图3,当BG=BC=13时,过G作GH⊥CD于H,交AB于M,
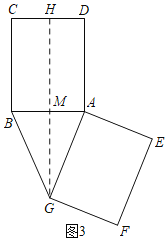
∵AG=BC=BG,
∴AM=BM=5,
Rt△AMG中,由勾股定理得:MG=![]() =
=![]() =12,
=12,
∵AB∥CD,
∴MH=BC=13,
∴GH=13+12=25,即点G到直线CD的距离是25;
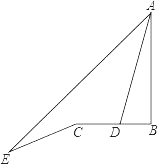
②如图4,过G作MH⊥CD于H,交AB于M,
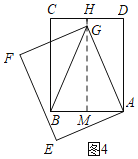
同理得GM=12,
∴GH=13﹣12=1,即点G到直线CD的距离是1;
综上,即点G到直线CD的距离是25或1.

 小题狂做系列答案
小题狂做系列答案