题目内容
如图,已知在△ABC中,AB=AC=6,cosB=
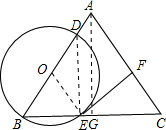
?点O在边AB上,⊙O过点B且分别与边AB、BC交 于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.
于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.
(1)求证:直线EF是⊙O的切线;
(2)求y关于x的函数关系式(不要求写自变量的取值范围).
| 1 |
| 3 |
 于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.
于点D、E,且EF⊥AC,垂足为F,设OB=x,CF=y.(1)求证:直线EF是⊙O的切线;
(2)求y关于x的函数关系式(不要求写自变量的取值范围).
(1)证明:连接OE
∵AB=AC
∴∠B=∠C
∵OB=OE
∴∠B=∠BEO
∴∠C=∠BEO
∴AC∥OE
∵EF⊥CA
∴EF⊥OE
点E在⊙O上
直线EF是⊙O的切线;
(2)过点A作AG⊥BC,垂足为G,
∴BG=
AB=2.
∵AB=AC,
∴BC=2BG=4.
∵OB=x,
∴BD=2x.
∵BD是⊙O的直径,
∴∠DEB=90°.
∵cosB=
=
,
∵OB=x,
∴BD=2x,
∴BE=
x,
∴CE=BC-BE=4-
x.
∵△BDE∽△CEF,
∴
=
,
∴y=-
x+
.
∵AB=AC
∴∠B=∠C
∵OB=OE
∴∠B=∠BEO
∴∠C=∠BEO
∴AC∥OE
∵EF⊥CA
∴EF⊥OE
点E在⊙O上
直线EF是⊙O的切线;
(2)过点A作AG⊥BC,垂足为G,
∴BG=
| 1 |
| 3 |
∵AB=AC,
∴BC=2BG=4.
∵OB=x,
∴BD=2x.
∵BD是⊙O的直径,
∴∠DEB=90°.
∵cosB=
| 1 |
| 3 |
| BE |
| BD |
∵OB=x,
∴BD=2x,
∴BE=
| 2 |
| 3 |
∴CE=BC-BE=4-
| 2 |
| 3 |
∵△BDE∽△CEF,
∴
| BD |
| CE |
| BE |
| CF |
∴y=-
| 2 |
| 9 |
| 4 |
| 3 |


练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目


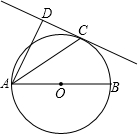




 是切点,
是切点, BM于N,AN的延长线交BC于D,直线AB交⊙A于P,K两点,作MT⊥BC于T.
BM于N,AN的延长线交BC于D,直线AB交⊙A于P,K两点,作MT⊥BC于T.