题目内容
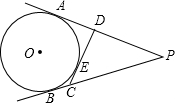
已知：如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=130°，过D点的切线PD与直线AB交于P点，则∠ADP的度数为（ ）
| A．40° | B．45° | C．50° | D．65° |
连接BD，
∵∠DAB=180°-∠C=50°，AB是直径，
∴∠ADB=90°，∠ABD=90°-∠DAB=40°，
∵PD是切线，
∴∠ADP=∠B=40°．
故选A．
∵∠DAB=180°-∠C=50°，AB是直径，
∴∠ADB=90°，∠ABD=90°-∠DAB=40°，
∵PD是切线，
∴∠ADP=∠B=40°．
故选A．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
