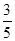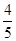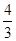题目内容
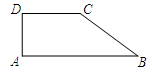
如图，点E是矩形ABCD中CD边上一点，⊿BCE沿BE折叠为⊿BFE,点F落在AD上.
(1)求证：⊿ABE∽⊿DFE;(2)若sin∠DFE=
,求tan∠EBC的值.
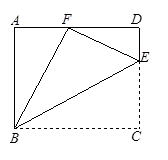
(1)求证：⊿ABE∽⊿DFE;(2)若sin∠DFE=
,求tan∠EBC的值.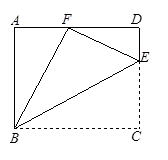(1)详见解析；(2) 
试题解析（1）证明：∵四边形ABCD是矩形
∴∠A=∠D=∠C=90°
∵⊿BCE沿BE折叠为⊿BFE
∴∠BFE=∠C=90°
∴∠AFB+∠DFE=180°-∠BFE=90°
又∠AFB+∠ABF=90°
∴∠ABF=∠DFE
∴⊿ABE∽⊿DFE
(2)解：在Rt⊿DEF中，sin∠DFE=
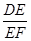=∴设DE=a,EF=3a,DF=
=2
a ∵⊿BCE沿BE折叠为⊿BFE
∴CE="EF=3a,CD=DE+CE=4a,AB=4a," ∠EBC=∠EBF
又由（1）⊿ABE∽⊿DFE，∴
=
=
=∴tan∠EBF=
=tan ∠EBC=tan∠EBF=
练习册系列答案
初中学业考试导与练系列答案
相关题目
．
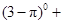
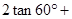
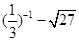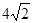，∠ACB = 45°．
