题目内容
【题目】如图,抛物线y=-x2+bx+3与x轴交于A,B两点,与y轴交于点C,其中点A(-1,0).过点A作直线y=x+c与抛物线交于点D,动点P在直线y=x+c上,从点A出发,以每秒![]() 个单位长度的速度向点D运动,过点P作直线PQ∥y轴,与抛物线交于点Q,设运动时间为t(s).
个单位长度的速度向点D运动,过点P作直线PQ∥y轴,与抛物线交于点Q,设运动时间为t(s).
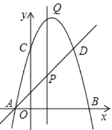
(1)直接写出b,c的值及点D的坐标;
(2)点 E是抛物线上一动点,且位于第四象限,当△CBE的面积为6时,求出点E 的坐标;
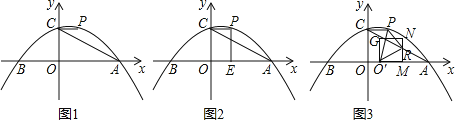
(3)在线段PQ最长的条件下,点M在直线PQ上运动,点N在x轴上运动,当以点D、M、N为顶点的三角形为等腰直角三角形时,请求出此时点N的坐标.
【答案】(1)b=2,c=1,D(2,3);(2)E(4,-5) ;(3)N(2,0),N(-4,0),N(-2.5,0),N(3.5,0)
【解析】
(1)将点A分别代入y=-x2+bx+3,y=x+c中求出b、c的值,确定解析式,再解两个函数关系式组成的方程组即可得到点D的坐标;
(2))过点E作EF⊥y轴,设E(x,-x2+2x+3),先求出点B、C的坐标,再利用面积加减关系表示出△CBE的面积,即可求出点E的坐标.
(3)分别以点D、M、N为直角顶点讨论△MND是等腰直角三角形时点N的坐标.
(1)将A(-1,0)代入y=-x2+bx+3中,得-1-b+3=0,解得b=2,
∴y=-x2+2x+3,
将点A代入y=x+c中,得-1+c=0,解得c=1,
∴y=x+1,
解![]() ,解得
,解得![]() ,
,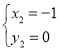 (舍去),
(舍去),
∴D(2,3).
∴b= 2 ,c= 1 ,D(2,3).
(2)过点E作EF⊥y轴,
设E(x,-x2+2x+3),
当y=-x2+2x+3中y=0时,得-x2+2x+3=0,解得x1=3,x2=-1(舍去),
∴B(3,0).
∵C(0,3),
∴![]() ,
,
∴![]() ,
,
解得x1=4,x2=-1(舍去),
∴E(4,-5).
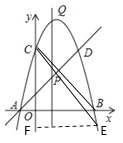
(3)∵A(-1,0),D(2,3),
∴直线AD的解析式为y=x+1,
设P(m,m+1),则Q(m,-m2+2m+3),
∴线段PQ的长度h=-m2+2m+3-(m+1)=![]() ,
,
∴当![]() =0.5,线段PQ有最大值.
=0.5,线段PQ有最大值.
当∠D是直角时,不存在△MND是等腰直角三角形的情形;
当∠M是直角时,如图1,点M在线段DN的垂直平分线上,此时N1(2,0);
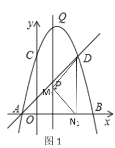
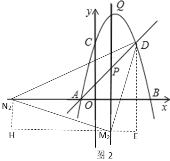
当∠M是直角时,如图2,作DE⊥x轴,M2E⊥HE,N2H⊥HE,
∴∠H=∠E=90,
∵△M2N2D是等腰直角三角形,
∴N2M2=M2D,∠N2M2D=90![]() ,
,
∵∠N2M2H=∠M2DE,
∴△N2M2H≌△M2DE,
∴N2H=M2E=2-0.5=1.5,M2H=DE,
∴E(2,-1.5),
∴M2H=DE=3+1.5=4.5,
∴ON2=4.5-0.5=4,
∴N2(-4,0);
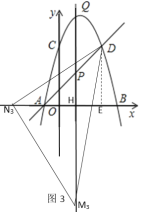
当∠N是直角时,如图3,作DE⊥x轴,
∴∠N3HM3=∠DEN3=90![]() ,
,
∵△M3N3D是等腰直角三角形,
∴N3M3=N3D,∠DN3M3=90![]() ,
,
∵∠DN3E=∠N3M3H,
∴△DN3E≌△N3M3H,
∴N3H=DE=3,
∴N3O=3-0.5=2.5,
∴N3(-2.5,0);
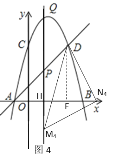
当∠N是直角时,如图4,作DE⊥x轴,
∴∠N4HM4=∠DEN4=90![]() ,
,
∵△M4N4D是等腰直角三角形,
∴N4M4=N4D,∠DN4M4=90![]() ,
,
∵∠DN4E=∠N4M4H,
∴△DN4E≌△N4M4H,
∴N4H=DE=3,
∴N4O=3+0.5=3.5,
∴N4(3.5,0);
综上,N(2,0),N(-4,0),N(-2.5,0),N(3.5,0).

 步步高达标卷系列答案
步步高达标卷系列答案