题目内容
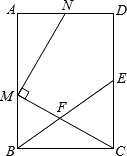
【题目】如图，已知抛物线y=x2+bx+c的图象与x轴的一个交点为B（5，0），另一个交点为A，且与y轴交于点C（0，5）．
（1）求直线BC与抛物线的解析式；
（2）若点M是抛物线在x轴下方图象上的一动点，过点M作MN∥y轴交直线BC于点N，求MN的最大值；
（3）若点P是抛物线在x轴下方图象上任意一点，以BC为边作平行四边形CBPQ，当平行四边形CBPQ的面积为30时，求点P的坐标．
【答案】（1）直线BC的解析式为y=﹣x+5．抛物线的解析式y=x2﹣6x+5；（2）
；（3）点P的坐标为（2，﹣3），（3，﹣4）．
【解析】
试题分析：（1）根据待定系数法，可得函数解析式，
（2）根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得二次函数，根据二次函数的性质，可得答案；
（3）根据平行四边形的面积，可得BD的长，根据等腰直角三角形，可得E点坐标，根据待定系数法，可得PQ的解析式，根据解方程组，可得答案．
试题解析: （1）设直线BC的解析式为y=kx+m，将B（5，0），C（0，5）代入，得
，解得
．
∴直线BC的解析式为y=﹣x+5．
将B（5，0），C（0，5）代入y=x2+bx+c，得
，解得
．
∴抛物线的解析式y=x2﹣6x+5；
（2）∵点M是抛物线在x轴下方图象上的动点，
∴设M（m，m2﹣6m+5）．
∵点N是直线BC上与点M横坐标相同的点，
∴N（m，m+5）．
∵当点M在抛物线在x轴下方时，N的纵坐标总大于M的纵坐标．
∴MN=﹣m+5﹣（m2﹣6m+5）=﹣m2+5m=﹣（m﹣
）2+．
∴MN的最大值是．
（3）如图
，
设平行四边形CBPQ的边BC上的高为BD，则BC⊥BD，可求BC=5
，
由平行四边形CBPQ的面积为30可得，BC×BD=30，从而BD=3．
设直线PQ交x轴于E点，
∵BC⊥BD，∠OBC=45°，
∴∠EBD=45°，△EBD为等腰直角三角形，BE=BD=6．
∵B（5，0），
∴E（﹣1，0）．
设直线PQ的解析式为y=﹣x+s，将E点坐标代入函数解析式，得
0=﹣（﹣1）+s，
解得s=﹣1，
从而直线PQ的解析式为y=﹣x﹣1．
联立直线与抛物线，得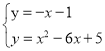
，
解得
，
，
故点P的坐标为（2，﹣3），（3，﹣4）．
