题目内容
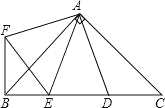
【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣8，3），B（﹣4，0），C（﹣4，3），∠ABC=α°．抛物线y=
x2+bx+c经过点C，且对称轴为x=﹣
，并与y轴交于点G．
（1）求抛物线的解析式及点G的坐标；
（2）将Rt△ABC沿x轴向右平移m个单位，使B点移到点E，然后将三角形绕点E顺时针旋转α°得到△DEF．若点F恰好落在抛物线上．①求m的值；
②连接CG交x轴于点H，连接FG，过B作BP∥FG，交CG于点P，求证：PH=GH．
【答案】（1）y=
x2+
x
，点G（0，-
）；（2）①
；②证明见解析.
【解析】试题分析：（1）把点C坐标代入y=
x2+bx+c得一方程，用对称轴公式得另一方程，组成方程组求出解析式，并求出G点的坐标；（2）①作辅助线，构建直角△DEF斜边上的高FM，利用直角三角形的面积相等和勾股定理可表示F的坐标，根据点F在抛物线上，列方程求出m的值；②F点和G点坐标已知，可以求出直线FG的方程，那么FG和x轴的交点坐标（设为Q）可以知道，C点坐标已知，CG的方程也可以求出，那么H点坐标可以求出，可以证明△BPH和△QGH全等．
试题解析：（1）根据题意得： 
解得： 
∴抛物线的解析式为：y=
x2+
x﹣
，点G（0，﹣
）；
（2）①过F作FM⊥y轴，交DE于M，交y轴于N，
由题意可知：AC=4，BC=3，则AB=5，FM=
，
∵Rt△ABC沿x轴向右平移m个单位，使B点移到点E，
∴E（﹣4+m，0），OE=MN=4﹣m，FN=
﹣（4﹣m）=m﹣
，
在Rt△FME中，由勾股定理得：EM=
=
，
∴F（m﹣
， 
），
∵F抛物线上，
∴
=
（m﹣
）2+
（m﹣
）﹣
，
5m2﹣8m﹣36=0，
m1=﹣2（舍），
；
②F（
， 
），
∴F（2， 
），
易求得FG的解析式为：y=
x﹣
，
CG解析式为：y=﹣
x﹣
，
∴
x﹣
=0，x=1，则Q（1，0），
﹣
x﹣
=0，x=﹣1.5，则H（﹣1.5，0），
∴BH=4﹣1.5=2.5，HQ=1.5+1=2.5，
∴BH=QH，
∵BP∥FG，
∴∠PBH=∠GQH，∠BPH=∠QGH，
∴△BPH≌△QGH，
∴PH=GH．
