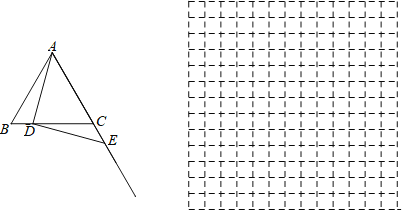题目内容
【题目】解下列方程：
（1）
；
（2）
；
（3）（x+1）（x+2）（x+3）（x+4）＝120；
【答案】（1）x1= 1，x2＝
，x3＝
．（2）x1＝8，x2＝﹣1，x3＝﹣8，x4＝1．（3）x1＝﹣6，x2＝1．
【解析】
（1）把原方程变形为
+1+
＝
，设y＝，可得分式方程，解分式方程后解两个一元二次方程即可得答案；（2）设x2+2x﹣8＝y，把原方程变形为
+
+
＝0，去分母后可得y＝9x或y＝﹣5x，代入x2+2x﹣8＝y，解两个一元二次方程即可得答案；（3）根据题意可得[（x+1）（x+4）][（x+2）（x+3）]＝120，即（x2+5x+4）（x2+5x+6）＝120，设x2+5x+4＝y，解关于y的一元二次方程求出y值，代入x2+5x+4＝y，解两个一元二次方程即可得答案.
（1）原方程可变形为+1+＝，
令y＝，则原方程可变为y+＝
，
解得y1＝
，y2＝
．
当y1＝时，＝，解得x＝1；
当y2＝时，＝，解得x＝
．
经检验：x＝1或都是原方程的解．
故原方程的解为x1＝1，x2＝，x3＝
．
（2）设x2+2x﹣8＝y，则原方程可化为：++＝0，
方程的两边同乘y（y+9x）（y﹣15x），整理得y2﹣4xy﹣45x2＝0，
解得y＝9x或y＝﹣5x．
当y＝9x时，x2+2x﹣8＝9x，x2﹣7x﹣8＝0，解得x1＝8，x2＝﹣1；
当y＝﹣5x时，x2+2x﹣8＝﹣5x，x2+7x﹣8＝0，解得x3＝﹣8，x4＝1．
经检验：x1＝8，x2＝﹣1，x3＝﹣8，x4＝1都是原方程的解．
故原方程的解为x1＝8，x2＝﹣1，x3＝﹣8，x4＝1．
（3）[（x+1）（x+4）][（x+2）（x+3）]＝120，
（x2+5x+4）（x2+5x+6）＝120，
设x2+5x+4＝y，则y（y+2）＝120，
∴y2+2y﹣120＝0，
解得y＝10或y＝﹣12．
当y＝10时，x2+5x+4＝10，x2+5x﹣6＝0，解得x1＝﹣6，x2＝1；
当y＝﹣12时，x2+5x+4＝﹣12，x2+5x+16＝0，△＝25﹣64＝﹣39＜0，故此方程无实根．
故原方程的解为x1＝﹣6，x2＝1．
智能训练练测考系列答案
计算高手系列答案【题目】在平面直角坐标系xOy中，有“抛物线系”y＝－（x－m）2+4m－3，顶点为点P，这些抛物线的形状与抛物线 y＝－x2 相同，但顶点位置不同．
（1）填写下表，并说出：在m取不同数值时，点P位置的变化具有什么特征？
m的值 | … | －1 | 0 | 1 | 2 | … |
点P坐标 | … | … |
（2）若抛物线的对称轴是直线x＝1，则可确定m的值．点M（p，q）为此抛物线上的一个动点，且﹣1＜p＜2，而直线y＝kx－4（k≠0）始终经过点M．
①求此抛物线与x轴的交点坐标；
②求k的取值范围．
（3）若点Q在x轴上，点S（0，－1）在y轴上，点R在坐标平面内，且以点P，Q，R，S为顶点的四边形是正方形，试直接写出所有点Q的坐标．
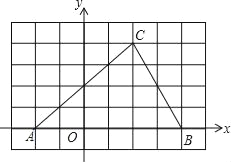
【题目】如图，在等边
中，
，点D是线段BC上的一动点，连接AD，过点D作
，垂足为D，交射线AC与点
设BD为xcm，CE为ycm．
小聪根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行了探究．
下面是小聪的探究过程，请补充完整：
通过取点、画图、测量，得到了x与y的几组值，如下表：
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
|
|
|
| ___ |
| 0 |
|
|
|
| 0 |
说明：补全表格上相关数值保留一位小数
建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；
结合画出的函数图象，解决问题：当线段BD是线段CE长的2倍时，BD的长度约为_____cm．
