题目内容
【题目】在平面直角坐标系xOy中,有“抛物线系”y=-(x-m)2+4m-3,顶点为点P,这些抛物线的形状与抛物线 y=-x2 相同,但顶点位置不同.
(1)填写下表,并说出:在m取不同数值时,点P位置的变化具有什么特征?
m的值 | … | -1 | 0 | 1 | 2 | … |
点P坐标 | … | … |
(2)若抛物线的对称轴是直线x=1,则可确定m的值.点M(p,q)为此抛物线上的一个动点,且﹣1<p<2,而直线y=kx-4(k≠0)始终经过点M.
①求此抛物线与x轴的交点坐标;
②求k的取值范围.
(3)若点Q在x轴上,点S(0,-1)在y轴上,点R在坐标平面内,且以点P,Q,R,S为顶点的四边形是正方形,试直接写出所有点Q的坐标.
【答案】(1)点P的位置始终在同一条直线上;(2)k<-1或k>2;(3)点Q的坐标有:(3,0),(-2,0),(![]() ,0),(-6,0),(
,0),(-6,0),(![]() ,0),(-
,0),(-![]() ,0).
,0).
【解析】
(1)由抛物线系y=-(x-m)2+4m-3,可得顶点P的坐标为(m,4m-3),把m=-1、0、1、2一次代入4m-3,即可求出相应的纵坐标,结果填表内,通过描点发现点P的位置始终在同一条直线上;(2)①根据对称轴是直线x=1,而抛物线顶点式y=-(x-m)2+4m-3中对称轴是直线x=m,所以m=1,从而求得抛物线的解析式;把y=0代入解析式即可求出与x轴交点坐标;②因为﹣1<p<2,所以把x=-1、2分别代入抛物线的解析式,解得y=-3、0,可得点M在抛物线上点(-1,-3 ),(2,0)之间运动,不包含此两点,再把此两点的坐标分别代入直线y=kx-4(k≠0)可得两个k的值,从而求得k的取值范围; (3)根据正方形的性质进行分类讨论可得结果.
解:(1)
m的值 | … | -1 | 0 | 1 | 2 | … |
点P坐标 | … | (-1,-7) | (0,-3) | (1,1) | (2,5) | … |
可通过描点得出:点P的位置始终在同一条直线上;
(2)①∵抛物线的对称轴为x=1,∴m=1,
∴抛物线的表达式为:y=﹣x2+2x;
当y=0时,﹣x2+2x=0,∴x1=0,x2=2,
∴抛物线与x轴的交点坐标是:(0,0),(2,0);
② 当﹣1<p<2时,结合图象,可知点M在运动中的边界点为:(-1,-3 ),(2,0);
当过(-1,﹣3)时,代入 y=kx﹣4,k=-1;
当过(2,0)时,代入 y=kx﹣4,k=2;
综上所述:k<-1或k>2;
(3)点Q的坐标有:(3,0),(-2,0),(![]() ,0),(-6,0),(
,0),(-6,0),(![]() ,0),(-
,0),(-![]() ,0).
,0).
理由:
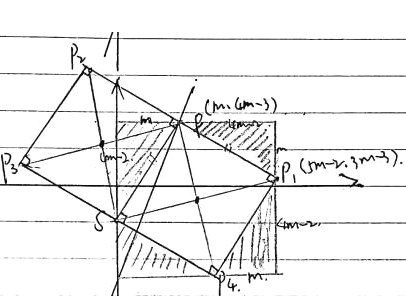
∵S(0,-1),P(m,4m-3)
∴①当SP为正方形的边长时,以SP为边向两边作正方形,如图,易证图中阴影三角形全等,解得P1(5m-2,3m-3),由中点公式得P2(2-3m,5m-3),由全等求得P4(4m-2,-m-1),P3(2-4m,-1+m).
当P1、P2、P3、P4中有一点落在x轴上时即可满足条件,
当P1落在x轴上时,3m-3=0,m=1, 此时Q(3,0)
当P2落在x轴上时,5m-3=0,m= ![]() ,此时Q(
,此时Q(![]() ,0)
,0)
当P3落在x轴上时,-1+ m=0,m=1,此时Q(-2,0)
当P4落在x轴上时,-m-1=0,m=-1,此时Q(-6,0)
②当SP为对角线时,另外两点的坐标即为图中两正方形的中心坐标,分别为(![]() m-1,
m-1, ![]() m-2),(1-
m-2),(1-![]() m,
m,![]() m-2).
m-2).
当![]() m-2=0时,m=
m-2=0时,m=![]() ,此时Q(
,此时Q(![]() ,0)
,0)
当![]() m-2时,m=
m-2时,m=![]() ,此时Q(-
,此时Q(-![]() ,0)
,0)
综上所述,Q点坐标为:(3,0),(-2,0),(![]() ,0),(-6,0),(
,0),(-6,0),(![]() ,0),(-
,0),(-![]() ,0).
,0).

【题目】某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
年度 | 2009 | 2010 | 2011 | 2012 |
投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
(1)试判断:从上表中的数据看出,y与x符合你学过的哪个函数模型?请说明理由,并写出它的解析式.
(2)按照上述函数模型,若2013年已投入技改资金5万元
①预计生产成本每件比2012年降低多少元?
②如果打算在2013年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?
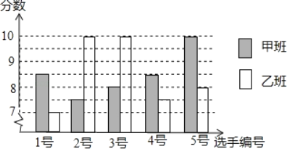
【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
(1)根据如图填写如表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8.5 | 10 | 1.6 |
(2)根据如表数据,分析哪个班的成绩较好,请详细说明.
【题目】在不透明的袋子中有四张标有数字1,2,3,4的卡片,小明、小华两人按照各自的规则玩抽卡片游戏。
小明画出树形图如下:

小华列出表格如下:
第一次 第二次 | 1 | 2 | 3 | 4 |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | ① | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
回答下列问题:
(1)根据小明画出的树形图分析,他的游戏规则是:随机抽出一张卡片后 (填“放回”或“不放回”),再随机抽出一张卡片;
(2)根据小华的游戏规则,表格中①表示的有序数对为 ;
(3)规定两次抽到的数字之和为奇数的获胜,你认为淮获胜的可能性大?为什么?