Question

【题目】Rt△ABC中，∠ACB＝90°，AC＝BC＝6，动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动，到达点C停止运动．设运动时间为t秒

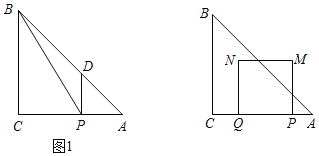
（1）如图1，过点P作PD⊥AC，交AB于D，若△PBC与△PAD的面积和是△ABC的面积的，求t的值；

（2）点Q在射线PC上，且PQ＝2AP，以线段PQ为边向上作正方形PQNM．在运动过程中，若设正方形PQNM与△ABC重叠部分的面积为8，求t的值．

Answer 1

【答案】（1）t1＝2，t2＝4；（2）t的值为或2时，重叠面积为8．

【解析】

（1）先求出△ABC的面积，然后根据题意可得AP＝t，CP＝6﹣t，然后再△PBC与△PAD的面积和是△ABC的面积的，列出方程、解方程即可解答；

（2）根据不同时间段分三种情况进行解答即可.

（1）∵Rt△ABC中，∠ACB＝90°，AC＝BC＝6，

∴S△ABC＝×6×6＝18，

∵AP＝t，CP＝6﹣t，

∴△PBC与△PAD的面积和＝t2+×6×（6﹣t），

∵△PBC与△PAD的面积和是△ABC的面积的，

∴t2+×6×（6﹣t）＝18×，

解之，得t1＝2，t2＝4；

（2）∵AP＝t，PQ＝2AP，

∴PQ＝2t，

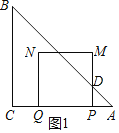
①如图1，当0≤t≤2时，S＝（2t）2﹣t2＝t2＝8，

解得：t1＝，t2＝﹣（不合题意，舍去），

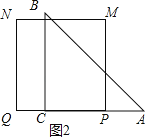
②如图2，当2≤t≤3时，S＝×6×6﹣t2﹣（6﹣2t）2＝12t﹣t2＝8，

解得：t1＝4（不合题意，舍去），t2＝（不合题意，舍去），

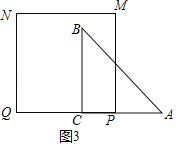
③如图3，当3≤t≤6时，S＝ 6×6﹣t2＝8，

解得：t1＝2，t 2＝﹣2（不合题意，舍去），

综上，t的值为或2时，重叠面积为8．