题目内容
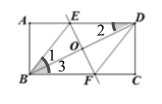
【题目】如图，在矩形ABCD中，BD的垂直平分线交AD于E，交BC于F，连接BE 、DF.
（1）判断四边形BEDF的形状，并说明理由；
（2）若AB=8，AD=16，求BE的长.
【答案】（1）四边形BEDF是菱形，理由见解析；（2）BE的长为10.
【解析】
（1）如图，由垂直平分线的性质可得
，再由等边对等角和平行线的性质得
，根据三线合一的性质可知
是等腰三角形，且
，从而得出四边形BEDF是菱形；
（2）设
，由题（1）的结论可得DE的长，从而可得AE的长，在
中利用勾股定理即可得.
（1）四边形BEDF是菱形，理由如下：
是BD的垂直平分线
∵四边形ABCD是矩形
，即BD是
的角平分线
是等腰三角形，且
∴四边形BEDF是菱形；
（2）设，由（1）可得
则
又∵四边形ABCD是矩形
在中，
，即
，解得
所以BE的长为10.
练习册系列答案
相关题目
【题目】2020年2月初，在抵御新冠肺炎的工作中，全国各地口罩严重供应不足，某乡镇企业缝纫车间立即转岗做口罩以供应本地志愿者和卫生系统，该车间有技术工人15人，生产部为了合理制定口罩的日生产定额，统计了15人某天加工口罩数如下：
车间15名工人某一天加工口罩个数统计表
加工零件数/个 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
（1）求这一天15名工人加工口罩数的平均数、中位数和众数．
（2）为了提高大多数工人的积极性，管理者准备试行“每天定额生产，超产有奖”的措施，假如你是管理者，从平均数、中位数、众数的角度进行分析，你将如何确定这个“定额”？
