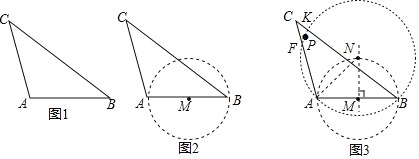
题目内容
【题目】已知![]() ,
,![]() ,
,![]() ,在
,在![]() 的延长线上任取一点
的延长线上任取一点![]() ,过点
,过点![]() 作
作![]() 的平行线交
的平行线交![]() 的延长线于点
的延长线于点![]() .
.
(1)当![]() 时,如图1,依题意补全图形,直接写出
时,如图1,依题意补全图形,直接写出![]() ,
,![]() ,
,![]() 的数量关系;
的数量关系;
(2)当![]() 时,如图2,判断
时,如图2,判断![]() ,
,![]() ,
,![]() 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;
(3)当![]() 时(
时(![]() ),请写出
),请写出![]() ,
,![]() ,
,![]() 之间的数量关系并写出解题思路.
之间的数量关系并写出解题思路.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)先根据已知条件画出图形,再根据等边三角形的性质即可得出结论;
(2)如图2,过![]() 作
作![]() 交
交![]() 延长线于
延长线于![]() 点,易证四边形
点,易证四边形![]() 为平行四边形,
为平行四边形,![]() 为等腰直角三角形,则由等腰直角三角形的性质知
为等腰直角三角形,则由等腰直角三角形的性质知![]() ,进一步即可得出结论;
,进一步即可得出结论;
(3)由(2)可知四边形![]() 为平行四边形,
为平行四边形,![]() 为等腰三角形,过
为等腰三角形,过![]() 点作
点作![]() 于
于![]() 点,则
点,则![]() ,
,![]() ,然后在直角△BDN中,根据∠BDN的正弦可得BN、BD的关系,整理即可得出结论.
,然后在直角△BDN中,根据∠BDN的正弦可得BN、BD的关系,整理即可得出结论.
解:(1)图形如图1所示,
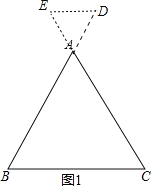
根据题意易知:△ABC与△ADE都是等边三角形,所以![]() ,
,![]() ,
,![]() 的数量关系为:
的数量关系为:![]() .
.
(2)结论:![]() .
.
理由:过![]() 作
作![]() 交
交![]() 延长线于
延长线于![]() 点.
点.
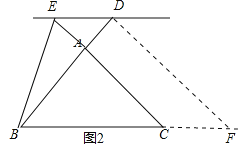
∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 为平行四边形.
为平行四边形.
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .∴
.∴![]() .
.
∴![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() 为等腰直角三角形.
为等腰直角三角形.
在![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
∴![]() .
.
(3)结论:![]() .
.
理由:如图,辅助线同(2),则由(2)可知四边形![]() 为平行四边形,
为平行四边形,![]() 为等腰三角形,
为等腰三角形,
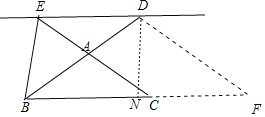
过![]() 点作
点作![]() 于
于![]() 点,则
点,则![]() ,
,![]() .
.
在![]() 中,
中,![]() ,∴
,∴![]() .
.
于是![]() .
.
故结论为:![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某林业部门统计某种树苗在本地区一定条件下的移植成活率,结果如表:
移植的棵数 | 300 | 700 | 1000 | 5000 | 15000 |
成活的棵数 | 280 | 622 | 912 | 4475 | 13545 |
成活的频率 | 0.933 | 0.889 | 0.912 | 0.895 | 0.903 |
根据表中的数据,估计这种树苗移植成活的概率为_____(精确到0.1);如果该地区计划成活4.5万棵幼树,那么需要移植这种幼树大约_____万棵.
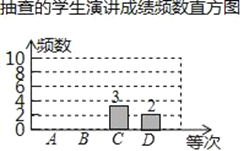
【题目】某校为庆祝“五四青年节”,在2018年4月底组织该校学生举办了“传承五四精神共建和谐社土会”的演讲比赛.为了解学生在演讲比赛中的成绩情况,学校随机抽取了部分学生的演讲比赛成绩进行统计(满分:100分,等次:A.优秀:90~100分;B.良好:80﹣89分;C.一般:60﹣79分;D.较差:60分以下,不含60分)得到如下不完整的图表:
等次 | 频数 | 频率 |
A | a | 0.25 |
B | b | 0.5 |
C | 3 | m |
D | 2 | 0.1 |
根据以上信息解答下列问题
(1)表中a=_____,b=_____,m=_______,并补全频数分布直方图;
(2)根据抽查学生演讲成绩频数统计表制作的扇形统计图中,表示C等次部分的扇形中心角的度数是_______;
(3)若A等次中有2名女生,其余为男生,学校准备从A等次学生中抽取2名学生组成演讲组合参加全市“五四青年杯”演讲比赛,求恰好抽取1名男生和1名女生的概率.