ћвƒњƒЏ»Ё
°Њћвƒњ°њƒ≥–£ќ™«м„£°∞ќеЋƒ«аƒкљЏ°±£ђ‘Џ2018ƒк4‘¬µ„„й÷ѓЄ√–£—І…ъЊў∞мЅЋ°∞іЂ≥–ќеЋƒЊЂ…сє≤љ®ЇЌ–≥…зЌЅїб°±µƒ—Ёљ≤±»»ь£Ѓќ™ЅЋљв—І…ъ‘Џ—Ёљ≤±»»ь÷–µƒ≥…Љ®«йњц£ђ—І–£Ћжїъ≥й»°ЅЋ≤њЈ÷—І…ъµƒ—Ёљ≤±»»ь≥…Љ®љш––Ќ≥Љ∆(¬ъЈ÷£Ї100Ј÷£ђµ»іќ£ЇA£Ѓ”≈–г£Ї90°Ђ100Ј÷£їB£ЃЅЉЇ√£Ї80©Б89Ј÷£їC£Ѓ“ї∞г£Ї60©Б79Ј÷£їD£Ѓљѕ≤о£Ї60Ј÷“‘ѕ¬£ђ≤їЇђ60Ј÷)µ√µљ»зѕ¬≤їЌк’ыµƒЌЉ±н£Ї
µ»іќ | ∆µ э | ∆µ¬ |
A | a | 0.25 |
B | b | 0.5 |
C | 3 | m |
D | 2 | 0.1 |
ЄщЊЁ“‘…ѕ–≈ѕҐљвірѕ¬Ѕ–ќ ћв
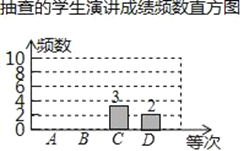
(1)±н÷–a£љ_____£ђb£љ_____£ђm£љ_______£ђ≤Ґ≤є»Ђ∆µ эЈ÷≤Љ÷±ЈљЌЉ£ї
(2)ЄщЊЁ≥й≤й—І…ъ—Ёљ≤≥…Љ®∆µ эЌ≥Љ∆±н÷∆„чµƒ…»–ќЌ≥Љ∆ЌЉ÷–£ђ±н ЊCµ»іќ≤њЈ÷µƒ…»–ќ÷––ƒљ«µƒґ» э «_______£ї
(3)»фAµ»іќ÷–”–2√ы≈Ѓ…ъ£ђ∆д”аќ™ƒ–…ъ£ђ—І–£„Љ±Єі”Aµ»іќ—І…ъ÷–≥й»°2√ы—І…ъ„й≥…—Ёљ≤„йЇѕ≤ќЉ”»Ђ –°∞ќеЋƒ«аƒк±≠°±—Ёљ≤±»»ь£ђ«у«°Ї√≥й»°1√ыƒ–…ъЇЌ1√ы≈Ѓ…ъµƒЄ≈¬ £Ѓ
°Њір∞Є°њ(1)5°Ґ10°Ґ0.15£ї(2)54°г£ї(3)![]() .
.
°Њљвќц°њ
£®1£©”…Dµ»іќ»Ћ эЉ∞∆д∆µ¬ «уµ√„№»Ћ э£ђ‘ўЄщЊЁ°∞∆µ¬ =∆µ э°¬„№ э°±«уљвњ…µ√ір∞Є£ї
£®2£©”√360°г≥Ћ“‘Cµ»іќµƒ∆µ¬ Љіњ…µ√£ї
£®3£©Ѕ– ч–ќЌЉЇуЉіњ…љЂЋщ”–«йњц»Ђ≤њЅ–Њў≥цјі£ђі”ґш«уµ√«°Ї√≥й÷–’вЅљ»ЋµƒЄ≈¬ .
(1)°я±їµч≤йµƒ„№»Ћ эќ™2°¬0.1£љ20£ђ
°аa£љ20°Ѕ0.25£љ5°Ґb£љ20°Ѕ0.5£љ10°Ґm£љ3°¬20£љ0.15£ђ
≤є»ЂЌЉ–ќ»зѕ¬£Ї
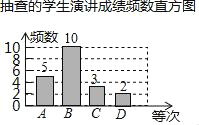
є ір∞Єќ™£Ї5°Ґ10°Ґ0.15£ї
(2)±н ЊCµ»іќ≤њЈ÷µƒ…»–ќ÷––ƒљ«µƒґ» э «360°г°Ѕ0.15£љ54°г£ђ
є ір∞Єќ™£Ї54°г£ї
(3)ї≠≥ц ч„іЌЉ»зѕ¬£Ї
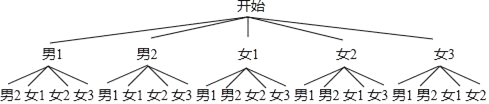
є≤”–20÷÷«йњц£ђ∆д÷–°∞«°Ї√ «1√ыƒ–…ъЇЌ1√ы≈Ѓ…ъ°±µƒ«йњц”–12÷÷£ђ
Ћщ“‘«°Ї√ «1√ыƒ–…ъЇЌ1√ы≈Ѓ…ъµƒЄ≈¬ ќ™![]() £љ
£љ![]() £Ѓ
£Ѓ

 “їѕя√ы ¶ћб”≈ ‘ЊнѕµЅ–ір∞Є
“їѕя√ы ¶ћб”≈ ‘ЊнѕµЅ–ір∞Є —фєв ‘Њнµ•‘™≤в ‘ЊнѕµЅ–ір∞Є
—фєв ‘Њнµ•‘™≤в ‘ЊнѕµЅ–ір∞Є