题目内容
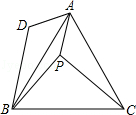
已知:如图,在等边△ABC中取点P,使得PA、PB、PC的长分别为3,4,5,将线段AP以点A为旋转中心顺时针旋转60°到线段AD,连接BD,下列结论:
①△ABD可以由△APC绕点A顺时针旋转60°得到;②点P与点D的距离为3; ③∠APB=150°;④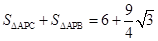
其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
①△ABD可以由△APC绕点A顺时针旋转60°得到;②点P与点D的距离为3; ③∠APB=150°;④
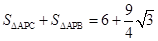
其中正确的结论有 ( )

A.1个 B.2个 C.3个 D.4个
D.
试题分析: 连PD,如图,
∵线段AP以点A为旋转中心顺时针旋转60°得到线段AD,∴AD=AP,∠DAP=60°,又∵△ABC为等边三角形,∴∠BAC=60°,AB=AC,∴∠DAB+∠BAP=∠PAC+∠BAP,∴∠DAP=∠PAC,∴△ABD可以由△APC绕点A顺时针旋转60°得到,所以①正确;
∵DA=PA,∠DAP=60°,∴△ADP为等边三角形,∴PD=PA=3,所以②正确;
在△PBD中,PB=4,PD=3,由①得到BD=PC=5,∵32+42=52,即PD2+PB2=BD2,∴△PBD为直角三角形,且∠BPD=90°,由②得∠APD=60°,∴∠APB=∠APD+∠BPD=60°+90°=150°,所以③正确;
∵△ADB≌△APC,∴S△ADB=S△APC,∴S△APC+S△APB=S△ADB+S△APB=S△ADP+S△BPD=
 ×32+
×32+ ×3×4=
×3×4= ,所以④正确.故选D.
,所以④正确.故选D.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 (0°<
(0°<
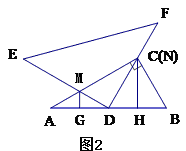




 的位置,若AE=1,BE=2,CE=3,则∠
的位置,若AE=1,BE=2,CE=3,则∠ = 度.
= 度.
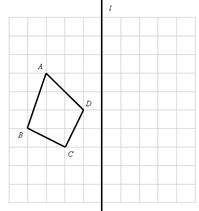
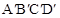 ,使四边形
,使四边形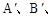
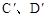 分别是点A、B、C、D的对称点;
分别是点A、B、C、D的对称点; 的长度。
的长度。