题目内容
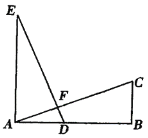
【题目】已知:如下图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.
求证:(1)△ADE![]() △BCA;
△BCA;
(2)ED⊥AC.
【答案】见解析.
【解析】
(1)求出∠EAD=∠CBA=90°,根据HL可证Rt△ADE≌Rt△BCA;
(2)由Rt△ADE≌Rt△BCA推出∠EDA=∠C,求出∠CAB+∠EDA=90°,根据三角形内角和定理求出∠AFD=90°即可
证明:(1)∵AE⊥AB,BC⊥AB,
∴∠EAD=∠CBA=90°,
在Rt△ADE和中Rt△ABC中,![]() ,
,
∴△ADE≌△BCA(HL),
(2) ∵△ADE≌△BCA(HL),
∴∠EDA=∠C,
又∵在Rt△ABC中,∠B=90°,
∴∠CAB+∠C=90°
∴∠CAB+∠EDA=90°,
∴∠AFD=90°,
∴ED⊥AC.

练习册系列答案
相关题目