题目内容
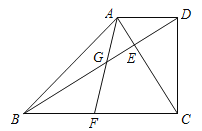
【题目】已知:如图,在梯形ABCD中,AD//BC,∠BCD=90,对角线AC、BD相交于点E,且AC⊥BD.
(1)求证:![]() ;
;
(2)点F是边BC上一点,联结AF,与BD相交于点G.如果∠BAF =∠DBF,求证:![]() .
.
【答案】(1)参见解析;(2)参见解析.
【解析】
试题分析:(1)利用已知条件和同角的余角相等得出∠ACD=∠CBD.再根据∠ADC=∠BCD=90.因为两角对应相等,两个三角形相似,所以△ACD∽△DBC.相似三角形对应边成比例,所以![]() ,从而得出结论;(2)利用平行线的性质和等量代换得出∠ADB=∠BAF.从而判定△ABG∽△DBA.得出
,从而得出结论;(2)利用平行线的性质和等量代换得出∠ADB=∠BAF.从而判定△ABG∽△DBA.得出![]() ,即
,即![]() ,又因为
,又因为![]() ,得出
,得出![]() ,代入前面的式子中即可得出结论.
,代入前面的式子中即可得出结论.
试题解析:(1)∵AD//BC,∠BCD=90,∴∠ADC=∠BCD=90.又∵AC⊥BD,∴∠ACD+∠ACB=∠CBD+∠ACB=90.∴∠ACD=∠CBD.∴△ACD∽△DBC.∴![]() ,即
,即![]() ;(2)∵AD//BC,∴∠ADB=∠DBF.∵∠BAF=∠DBF,∴∠ADB=∠BAF.∵∠ABG=∠DBA,∴△ABG∽△DBA.∴
;(2)∵AD//BC,∴∠ADB=∠DBF.∵∠BAF=∠DBF,∴∠ADB=∠BAF.∵∠ABG=∠DBA,∴△ABG∽△DBA.∴![]() .两边同时平方得:
.两边同时平方得:![]() .又由于△ABG∽△DBA,∴
.又由于△ABG∽△DBA,∴![]() .
.
∴![]() .∴
.∴![]() .
.

练习册系列答案
相关题目