Question

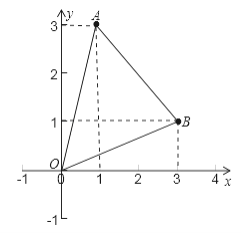
【题目】已知坐标平面内的三个点A（1，3），B（3，1），O（0，0），求△ABO的面积．

Answer 1

【答案】4．

【解析】

试题过A、B分别作y轴，x轴的垂线，根据“△ABO的面积=矩形OCDE的面积—△ACO的面积—△BEO的面积—△ABD的面积”计算出即可.

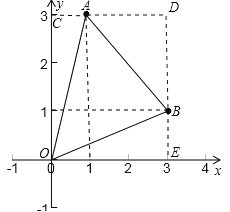
试题解析： 解：如图所示，过A，B分别作y轴，x轴的垂线，垂足为C，E，两线交于点D，

则C（0，3），D（3，3），E（3，0）．

又因为O（0，0），A（1，3），B（3，1），

所以OC=3，AC=1，OE=3，BE=1，

AD=DC﹣AC=3﹣1=2，

BD=DE﹣BE=3﹣1=2，

则四边形OCDE的面积为3×3=9，

△ACO和△BEO的面积都为×3×1=，

△ABD的面积为×2×2=2，

所以△ABO的面积为9﹣2×﹣2=4．