题目内容
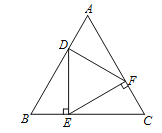
【题目】如图，等边△ABC的边长为6，点D为AB上一点，DE⊥BC于点E，EF⊥AC于点F，连接DF．若△DEF也是等边三角形，求AD的长．
【答案】2．
【解析】试题分析：先由△ABC是等边三角形和△DEF是等边三角形，用AAS证明△DEB≌△EFC，得到DB=EC，在Rt△DEB中，利用30度角所对直角边等于斜边的一半，即可得到BE的长，进而得到BD的长，即可得到结论．
试题解析：解：∵△ABC为等边三角形，∴∠B＝∠C＝60°．
∵△DEF为等边三角形，∴DE＝EF．
∵DE⊥BC，EF⊥AC，∴∠DEB＝∠EFC＝90°．
在△DEB和△EFC中，∵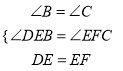
，∴△DEB≌△EFC（AAS），∴DB＝EC．
在Rt△DEB中，∠DEB＝90°，∠BDE＝90°－60°＝30°，∴BE＝
BD＝
EC．
∴
，∴
．∴
，∴
．
练习册系列答案
相关题目
【题目】小明抛硬币的过程(每枚硬币只有正面朝上和反面朝上两种情况)见下表，阅读并回答问题：
抛掷结果 | 10次 | 50次 | 500次 | 5000次 |
出现正面次数 | 3 | 24 | 258 | 2498 |
出现正面的频率 | 30% | 48% | 51.6% | 49.96% |
(1)从表中可知，当抛完10次时正面出现3次，正面出现的频率为30%，那么，小明抛完10次时，得到 次反面，反面出现的频率是 ；
(2)当他抛完5000次时，反面出现的次数是 ，反面出现的频率是 ；
(3)通过上表我们可以知道，正面出现的频数和反面出现的频数之和等于
，正面出现的频率和反面出现的频率之和等于 .
