题目内容
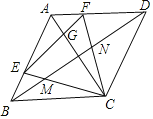
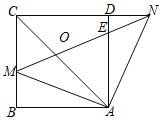
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,MN与边AD交于点E.
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE;
(3)MN和AC相交于O点,若BM=1,AB=3,试猜想线段OM,ON的数量关系并证明.
【答案】(1)见详解;(2)见详解;(3)ON=2OM,理由见详解
【解析】
(1)由正方形的性质可得AB=AD,由“ASA”可证△ABM≌△ADN,可得AM=AN;
(2)由题意可得∠CAM=∠NAD=22.5°,∠ACB=∠MNA=45°,即可证△AMC∽△AEN,即可证AM2=AEAC;
(3)先求出AM,进而求出MF=NF=BF=![]() ,再判断出△ABM∽△AFO,进而求出FO,即可得出结论.
,再判断出△ABM∽△AFO,进而求出FO,即可得出结论.
证明(1)∵四边形ABCD是正方形,
∴AB=AD,∠CAD=45°=∠ACB,∠BAD=90°=∠CDA=∠B,
∴∠BAM+∠MAD=90°,
∵∠MAN=90°,
∴∠MAD+∠DAN=90°,
∴∠BAM=∠DAN,
∵AD=AB,∠ABC=∠ADN=90°,
∴△ABM≌△ADN(ASA)
∴AM=AN;
(2)∵AM=AN,∠MAN=90°
∴∠MNA=45°,
∵∠CAD=2∠NAD=45°,
∴∠NAD=22.5°
∴∠CAM=∠MAN﹣∠CAD﹣∠NAD=22.5°
∴∠CAM=∠NAD,∠ACB=∠MNA=45°,
∴△AMC∽△AEN,
∴![]() ,
,
∴AMAN=ACAE,
∵AN=AM,
∴AM2=ACAE;
(3)ON=2OM,理由:如图,
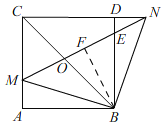
在Rt△ABM中,AM=1,AB=3,
根据勾股定理得,BM=![]() =
=![]() ,
,
过点B作BF⊥MN于F,
∴∠OFB=∠A=90°,
由(1)知,AM=AN,
∵∠MBN=90°,
∴FB=NF=MF=![]() =
=![]() ,∠MBF=45°,
,∠MBF=45°,
∵AC是正方形ABCD的对角线,
∴∠ABC=45°=∠MBF,
∴∠ABM=∠FBO,
∴△ABM∽△FBO,
∴![]() ,
,
∴![]() ,
,
∴FO=![]() ,
,
∴OM=MF﹣FO=![]() ,ON=NF+FO=
,ON=NF+FO=![]() ,
,
∴ON=2OM.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案