题目内容
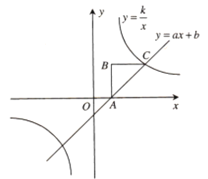
【题目】在平面直角坐标系xOy中，A(0，2)，B(m， m-2)，则AB+ OB的最小值是（ ）
A.
B.4C.
D.2
【答案】A
【解析】
如图，因为B（m，m-2），推出点B在直线y=x-2上，设直线y=x-2交x轴于D，交y轴于C，易知OC=OD=2，构造正方形OCDE，则E（2，-2），由AB+OB=AB+BE，AB+BE≥AE，推出AB+OB的最小值为AE．
如图，∵B（m，m-2），
∴点B在直线y=x-2上，设直线y=x-2交x轴于D，交y轴于C，易知OC=OD=2，构造正方形OCDE，则E（2，-2），
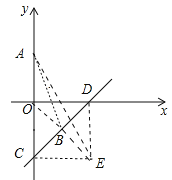
连接BE，AE．
∵四边形OCED是正方形，
∴OB=BE
∴AB+OB=AB+BE，
∵AB+BE≥AE，
∴AB+OB的最小值为AE，
在Rt△ACE中，AC=4，CE=2，
∴AE=
．
∴AB+OB的最小值为
，
故选：A．
练习册系列答案
阅读快车系列答案
相关题目
