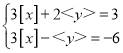题目内容
【题目】（1）观察下列各式：
……试用你发现的规律填空：
，
。
（2）请你用含有一个字母的等式将上面各式呈现的规律表示出来，并用所学数学知识说明你所写式子的正确性。
【答案】（1）192172＝4×18，482462＝4×47；（2）（n＋2）2n2＝4（n＋1）．
【解析】
（1）根据
由6242＝4×5，5界于4和6之间的正整数，
，7界于6和8之间的正整数，11292＝4×10，10界于11和9之间的正整数，可得出192172＝4×18，482462＝4×47；
（2）由（1）推出该规律为：（n＋2）2n2＝4（n＋1）．
（1）根据由6242＝4×5，5界于4和6之间的正整数，，7界于6和8之间的正整数，11292＝4×10，10界于11和9之间的正整数
∴可得出192172＝4×18，482462＝4×47；
（2）由（1）推出该规律为：（n＋2）2n2＝4（n＋1）．
故答案为：（1）192172＝4×18，482462＝4×47；（2）（n＋2）2n2＝4（n＋1）．
练习册系列答案
高效智能课时作业系列答案
相关题目
