Question

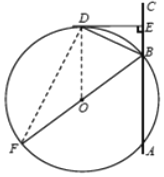
【题目】如图，BF为⊙O的直径，直线AC交⊙O于A，B两点，点D在⊙O上，BD平分∠OBC，DE⊥AC于点E．

（1）求证：直线DE是⊙O的切线；

（2）若 BF=10，sin∠BDE=，求DE的长．

Answer 1

【答案】（1）见解析；（2）4.

【解析】

试题分析：（1）先连接OD，根据∠ODB=∠DBE，即可得到OD∥AC，再根据DE⊥AC，可得OD⊥DE，进而得出直线DE是⊙O的切线；

（2）先连接DF，根据题意得到∠F=∠BDE，在Rt△BDF中，根据=sinF=sin∠BDE=，可得BD=2，在Rt△BDE中，根据sin∠BDE==，可得BE=2，最后依据勾股定理即可得到DE的长．

试题解析：（1）如图所示，连接OD，

∵OD=OB，∴∠ODB=∠OBD，

∵BD平分∠OBC，∴∠OBD=∠DBE，∴∠ODB=∠DBE，∴OD∥AC，

∵DE⊥AC，∴OD⊥DE，

∵OD是⊙O的半径，∴直线DE是⊙O的切线；

（2）如图，连接DF，

∵BF是⊙O的直径，∴∠FDB=90°，∴∠F+∠OBD=90°，

∵∠OBD=∠DBE，∠BDE+∠DBE=90°，∴∠F=∠BDE，

在Rt△BDF中，=sinF=sin∠BDE=，∴BD=10×=2，

∴在Rt△BDE中，sin∠BDE==，∴BE=2×=2，

∴在Rt△BDE中，DE==4．