题目内容
【题目】在平面直角坐标系中,点D是抛物线![]()
![]() 的顶点,抛物线与x轴交于点A,B(点A在点B的左侧).
的顶点,抛物线与x轴交于点A,B(点A在点B的左侧).
(1)求点A,B的坐标;
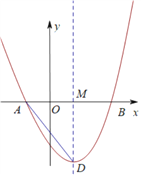
(2)若M为对称轴与x轴交点,且DM=2AM,求抛物线表达式;
(3)当30°<∠ADM<45°时,求a的取值范围.
【答案】(1)A(-1,0),B(3,0).(2)抛物线的表达式为![]() .(3)
.(3)![]() <a<
<a<![]() .
.
【解析】
(1)解关于x的方程![]() ,结合点A在点B的左侧,即可求得点A和点B的坐标;
,结合点A在点B的左侧,即可求得点A和点B的坐标;
(2)由(1)中结果易得抛物线的对称轴为直线x=1,顶点D坐标为(1,-4a),由此可得点M的坐标为(1,0),AM=2,这样结合DM=2AM即可得到关于a的方程,解方程求得a的值即可求得此时抛物线的解析式;
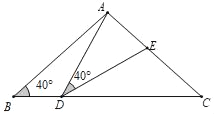
(3)画出图形如下图所示,由∠ADM=30°和∠ADM=45°可得![]() 和AM=DM,结合(2)中所得AM=2,MD=0-(-4a)=4a即可得到对应的关于a的方程,解方程即可求得对应的a的值.
和AM=DM,结合(2)中所得AM=2,MD=0-(-4a)=4a即可得到对应的关于a的方程,解方程即可求得对应的a的值.
(1)令y=0,得![]() ,
,
解得![]() ,x2=3.
,x2=3.
∴A(-1,0),B(3,0).
(2)∵抛物线![]() 与x轴的交点为A(-1,0),B(3,0),
与x轴的交点为A(-1,0),B(3,0),
∴抛物线对称轴为x=1,
∴AM=2,
∵DM=2AM,
∴DM=4.
∵当x=1时,y=-4a,
∴点D的坐标为(1,-4a),
∴0-(-4a)=4,解得a=1,
∴抛物线的表达式为![]() ;
;
(3)图下图所示,
当∠ADM=45°时,由题意可得AM=DM,
∵AM=2,DM=0-(-4a)=4a,
∴4a=2,解得:![]() ;
;
当∠ADM=30°时,由题意易得![]() ,
,
∵AM=2,DM=0-(-4a)=4a,
∴![]() ,解得:
,解得:![]() .
.
综上可得当30°<∠ADM<45°时,![]() .
.

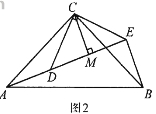
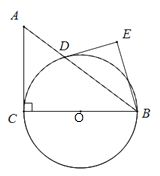
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以边BC为直径作⊙O,交AB于D,DE是⊙O的切线,过点B作DE的垂线,垂足为E.
(1)求证∠ABC=∠ABE;
(2)求DE的长.
【题目】为了解2018年某校九年级数学质量监控情况,随机抽取40名学生的数学成绩进行分析.
成绩统计如下.
93 | 92 | 84 | 55 | 85 | 82 | 66 | 75 | 88 | 67 |
87 | 87 | 37 | 61 | 86 | 61 | 77 | 57 | 72 | 75 |
68 | 66 | 79 | 92 | 86 | 87 | 61 | 86 | 90 | 83 |
90 | 18 | 70 | 67 | 52 | 79 | 86 | 71 | 61 | 89 |
2018年某校九年级数学质量监控部分学生成绩统计表:
分数段 | x<50 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
人数 | 2 | 3 | 9 | 13 |
平均数、中位数、众数如下表:
统计量 | 平均数 | 中位数 | 众数 |
分值 | 74.2 | 78 | 86 |
请根据所给信息,解答下列问题:
(1)补全统计表中的数据;
(2)用统计图将2018年某校九年级数学质量监控部分学生成绩表示出来;
(3)根据以上信息,提出合理的复习建议.
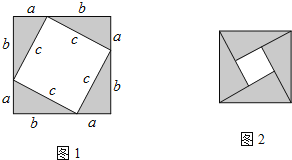
【题目】如图1,将边长为1的正方形ABCD压扁为边长为1的菱形ABCD.在菱形ABCD中,∠A的大小为α,面积记为S.

(1)请补全下表:
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
(2)填空:
由(1)可以发现正方形在压扁的过程中,菱形的面积随着∠A大小的变化而变化,不妨把菱形的面积S记为S(α).例如:当α=30°时,![]() ;当α=135°时,
;当α=135°时,![]() .由上表可以得到
.由上表可以得到![]() ( ______°);
( ______°);![]() ( ______°),…,由此可以归纳出
( ______°),…,由此可以归纳出![]() .
.
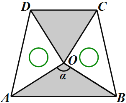
(3) 两块相同的等腰直角三角板按如图的方式放置,AD=![]() ,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).
,∠AOB=α,试探究图中两个带阴影的三角形面积是否相等,并说明理由(注:可以利用(2)中的结论).