题目内容
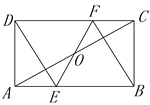
【题目】综合与探究：如图，二次函数
经过点B（4，0）和点E（-2，-3）两点，与x轴的另一个交点为A．点D是线段BE上的动点，过点D作DF⊥BE，交y轴于点F，交抛物线于点P．
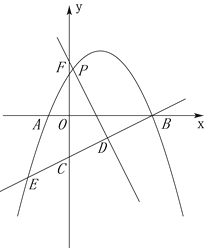
（1）求出抛物线和直线BE的解析式；
（2）当△DCF≌△BOC时，求出此时点D的坐标；
（3）设点P的横坐标为m．
①请写出线段PD的长度为（用含m的式子表示）；
②当m为何值时，线段PD有最大值，并写出其最大值为多少？
【答案】（1）
，y=
x-2；（2）点D的坐标为（
，
）或（
，
）；（3）①
；②当m=1时，PD有最大值为
．
【解析】
（1）设直线BE的解析式为y=kx+t，把B、E坐标分别代入
和y=kx+t，求出b、c、k、t的值即可得答案；
（2）根据BE解析式可得C点坐标，利用勾股定理可求出BC的长，当点F在点C上方时，由全等三角形得性质可得OC=CD，过点D作DH⊥OB，垂足为H，可得DH//OC，根据平行线分线段成比例定理可得
，可求出OH的长，代入BE解析式求出y值即可得点D坐标；同理可求出当点F在点C下方时点D的坐标；
（3）①过点P作PQ//FC，交BE于Q，根据抛物线及BE解析式可用m表示出P、Q坐标，即可表示出PQ得长，根据平行线得性质可得∠OCB=∠PQD，可得∠PQD得正弦值，利用∠PQD的正弦即可表示出PD的长；
②根据二次函数得性质即可得答案．
（1）把B（4，0），E（-2，-3）代入抛物线的解析式得：
，
解得b=
，c=2．
∴抛物线的解析式为，
设直线BE的解析式为y=kx+t，
∵B（4，0），E（-2，-3），
∴
，
解得k=，b=-2．
∴直线BE的解析式为y=x-2．
（2）当x=0时，y=x-2=-2．
∴C的坐标是（0，-2）
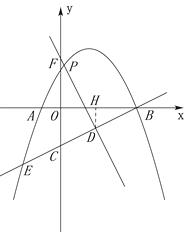
如图，当点F在点C上方时，
∵△DCF≌△OCB，
∴CD=OC=2．
∴BC=
，
过点D作DH⊥OB，垂足为H．
∴DH//OC，
∴．
∴
．
∴OH=．
把x=代入y=x-2得，y=．
∴点D的坐标为（，）．
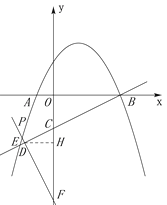
如图，当点F在点C下方时，
∵△DCF≌△OCB，
∴CD=OC=2．
过点D作DH⊥OF，垂足为H．
∴DH//OC，
∴
．
∴
．
∴DH=
把x=代入y=x-2得，y=．
∴点D的坐标为（，
）．
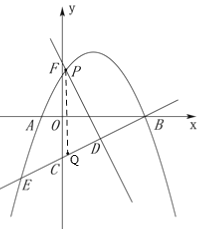
（3）①如图，过点P作PQ//FC，交BE于Q，
∴∠OCB=∠PQD，
∵sin∠PQD=sin∠OCB=
=
，
∵点P横坐标为m，
∴P（m，
），Q（m，
），
∴PQ=-（）=
，
∴PD=PQ·sin∠PQD=（）=．
②∵PD==
（m-1）2+，
∴当m=1时，PD有最大值．
