题目内容
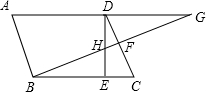如图，已知平行四边形ABCD中，∠DBC=45°，DE⊥BC于E，BF⊥CD于F，DE，BF交于H，BF，AD的延长线交于G，给出下列结论：①DB=| 2 |
| A、0个 | B、1个 | C、2个 | D、3个 |
分析：由题意可得，△BDE是等腰直角三角形，则DB=
BE；还可用AAS证明△BHE≌△DCE，则∠BHE=∠C=∠A，BH=CD=AB．故三个结论都正确．
| 2 |
解答：解：①正确，
∵∠DBC=45°，DE⊥BC，
∴DB=
BE．
②③正确，
∵AD∥BC，
∴∠AGB=∠HBE，
∴∠BHE=∠DCE，
又∵∠DBC=45°，DE⊥BC，
∴DE=BE，
∴△BHE≌△DCE，
∴DC=BH，
∴AB=BH．
故选D
∵∠DBC=45°，DE⊥BC，
∴DB=
| 2 |
②③正确，
∵AD∥BC，
∴∠AGB=∠HBE，
∴∠BHE=∠DCE，
又∵∠DBC=45°，DE⊥BC，
∴DE=BE，
∴△BHE≌△DCE，
∴DC=BH，
∴AB=BH．
故选D
点评：此题主要考查平行四边形的性质、等腰直角三角形的判定、全等三角形的判定，综合利用了勾股定理和直角三角形的性质．
练习册系列答案
相关题目
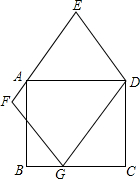CD的边长a等于点P，Q间的距离．
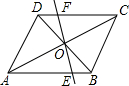如图，已知平行四边形ABCD的对角线AC，BD相交于点O，BD绕点O顺时针旋转交AB，DC于E，F．
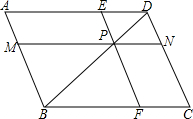交AB、CD、AD、BC于M、N、E、F，设a=PM•PE，b=PN•PF．
23、如图，已知平行四边形ABCD．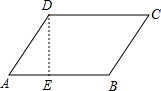
如图，已知平行四边形ABCD，作DE⊥AB，垂足为E，把三角形AED沿AB方向平移AB长个单位长度．