题目内容
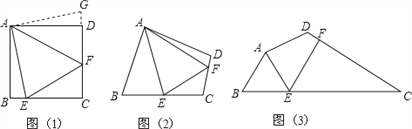
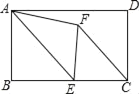
【题目】如图，矩形ABCD中，E为BC的中点，将△ABE沿直线AE折叠时点B落在点F处，连接FC，若∠DAF＝18°，则∠DCF＝_____度．
【答案】36 ．
【解析】
由折叠的性质得：FE＝BE，∠FAE＝∠BAE，∠AEB＝∠AEF，求出∠BAE＝∠FAE＝36°，由直角三角形的性质得出∠AEF＝∠AEB＝54°，求出∠CEF＝72°，求出FE＝CE，由等腰三角形的性质求出∠ECF＝54°，即可得出∠DCF的度数．
解：∵四边形ABCD是矩形，
∴∠BAD＝∠B＝∠BCD＝90°，
由折叠的性质得：FE＝BE，∠FAE＝∠BAE，∠AEB＝∠AEF，
∵∠DAF＝18°，
∴∠BAE＝∠FAE＝
×（90°﹣18°）＝36°，
∴∠AEF＝∠AEB＝90°﹣36°＝54°，
∴∠CEF＝180°﹣2×54°＝72°，
∵E为BC的中点，
∴BE＝CE，
∴FE＝CE，
∴∠ECF＝×（180°﹣72°）＝54°，
∴∠DCF＝90°﹣∠ECF＝36°.
故答案为36．
练习册系列答案
相关题目
