题目内容
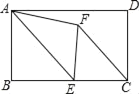
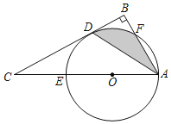
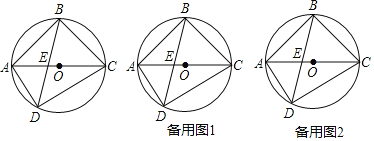
【题目】如图,四边形ABCD内接于⊙O,AC为直径,AC和BD交于点E,AB=BC.
(1)求∠ADB的度数;
(2)过B作AD的平行线,交AC于F,试判断线段EA,CF,EF之间满足的等量关系,并说明理由;
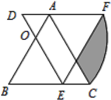
(3)在(2)条件下过E,F分别作AB,BC的垂线,垂足分别为G,H,连接GH,交BO于M,若AG=3,S四边形AGMO:S四边形CHMO=8:9,求⊙O的半径.
【答案】(1)45°;(2)EA2+CF2=EF2,理由见解析;(3)6![]()
【解析】
(1)由直径所对的圆周角为直角及等腰三角形的性质和互余关系可得答案;
(2)线段EA,CF,EF之间满足的等量关系为:EA2+CF2=EF2.如图2,设∠ABE=α,∠CBF=β,先证明α+β=45°,再过B作BN⊥BE,使BN=BE,连接NC,判定△AEB≌△CNB(SAS)、△BFE≌△BFN(SAS),然后在Rt△NFC中,由勾股定理得:CF2+CN2=NF2,将相关线段代入即可得出结论;
(3)如图3,延长GE,HF交于K,由(2)知EA2+CF2=EF2,变形推得S△ABC=S矩形BGKH,S△BGM=S四边形COMH,S△BMH=S四边形AGMO,结合已知条件S四边形AGMO:S四边形CHMO=8:9,设BG=9k,BH=8k,则CH=3+k,求得AE的长,用含k的式子表示出CF和EF,将它们代入EA2+CF2=EF2,解得k的值,则可求得答案.
解:(1)如图1,
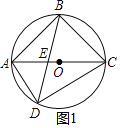
∵AC为直径,
∴∠ABC=90°,
∴∠ACB+∠BAC=90°,
∵AB=BC,
∴∠ACB=∠BAC=45°,
∴∠ADB=∠ACB=45°;
(2)线段EA,CF,EF之间满足的等量关系为:EA2+CF2=EF2.理由如下:
如图2,设∠ABE=α,∠CBF=β,
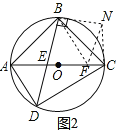
∵AD∥BF,
∴∠EBF=∠ADB=45°,
又∠ABC=90°,
∴α+β=45°,
过B作BN⊥BE,使BN=BE,连接NC,
∵AB=CB,∠ABE=∠CBN,BE=BN,
∴△AEB≌△CNB(SAS),
∴AE=CN,∠BCN=∠BAE=45°,
∴∠FCN=90°.
∵∠FBN=α+β=∠FBE,BE=BN,BF=BF,
∴△BFE≌△BFN(SAS),
∴EF=FN,
∵在Rt△NFC中,CF2+CN2=NF2,
∴EA2+CF2=EF2;
(3)如图3,延长GE,HF交于K,
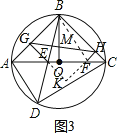
由(2)知EA2+CF2=EF2,
∴![]() EA2+
EA2+![]() CF2=
CF2=![]() EF2,
EF2,
∴S△AGE+S△CFH=S△EFK,
∴S△AGE+S△CFH+S五边形BGEFH=S△EFK+S五边形BGEFH,
即S△ABC=S矩形BGKH,
∴![]() S△ABC=
S△ABC=![]() S矩形BGKH,
S矩形BGKH,
∴S△GBH=S△ABO=S△CBO,
∴S△BGM=S四边形COMH,S△BMH=S四边形AGMO,
∵S四边形AGMO:S四边形CHMO=8:9,
∴S△BMH:S△BGM=8:9,
∵BM平分∠GBH,
∴BG:BH=9:8,
设BG=9k,BH=8k,
∴CH=3+k,
∵AG=3,
∴AE=3![]() ,
,
∴CF=![]() (k+3),EF=
(k+3),EF=![]() (8k﹣3),
(8k﹣3),
∵EA2+CF2=EF2,
∴![]() ,
,
整理得:7k2﹣6k﹣1=0,
解得:k1=﹣![]() (舍去),k2=1.
(舍去),k2=1.
∴AB=12,
∴AO=![]() AB=6
AB=6![]() ,
,
∴⊙O的半径为6![]() .
.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此九(2)班数学兴趣小组对本班同学天饮用饮品的情况进行了调查,发现大致可分为四种:A非碳酸饮料,B瓶装矿泉水,C碳酸饮料,D白开水.
根据统计结果绘制如下两个统计图,根据统计图提供的信息解答下列问题:
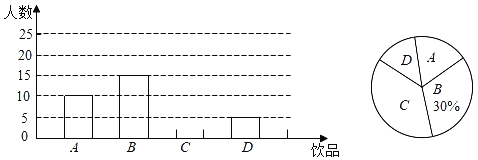
(1)九(2)班级有多少名同学?并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如表),则该班同学每天用于饮品的人均花费是多少元?
饮品名称 | 白开水 | 瓶装矿泉水 | 碳酸饮料 | 非碳酸饮料 |
平均价格(元/瓶) | 0 | 2 | 3 | 4 |
(3)为了养成良好的生活习惯,班主任决定在饮用白开水的5名同学(其中有两位班长记为a,b,其余三位记为c,d,e)中随机抽取2名作良好习惯监督员,请用列表法或画树状图的方法,求出抽到的2名同学都不是班长的概率.