题目内容
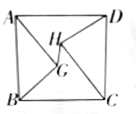
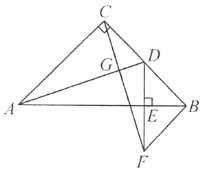
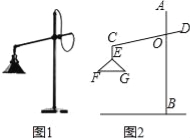
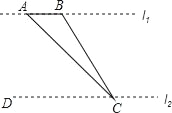
【题目】如图，在边长为1的正方形
中，对角线
，
相交于点
，点
，点
分别是
，
的中点，
交于点
，连接
，
，
，得到以下四个结论：①
，②
，③
，④
，其中正确的结论是________（填写序号）．
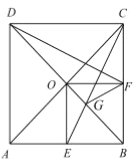
【答案】①③④
【解析】
根据正方形的性质、中位线的性质、全等三角形的性质以及判定定理、勾股定理、三角形外角的性质、相似三角形的性质以及判定定理进行分析即可．
∵四边形ABCD是正方形
∴
∵点
，点
分别是
，
的中点
∴
∴
在△DCF和△CBE中
∴
∴
∴
∴
∴
∴
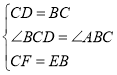
，故①正确
由勾股定理得
∵四边形ABCD是正方形
∴
，
，
，
∵O是AC中点，F是BC中点
∴
∴
在△BEG和△BFG中
∴
∴
∴
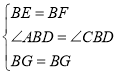
由勾股定理得
∴
∴
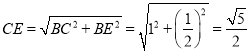
，故②错误
∵
∴
在△DBF和△CAE中
∴
∴
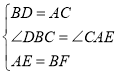
根据三角形外角的性质可得
∴
∴
，故③正确
作
与BC交于I
∵
∴
∵
∴
在△CGI和△CEB中
∴
∴
∴
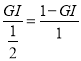
解得
∴
，故④正确
综上所述：①③④正确．
故答案为：①③④．
练习册系列答案
相关题目
【题目】我市少体校为了从甲、乙两名运动员中选出一名运动员参加省运动会百米比赛，组织了选拔测试，分别对两人进行了五次测试，成绩（单位：秒）以及平均数、方差如表：
甲 | 13 | 13 | 14 | 16 | 18 | x | S |
乙 | 14 | 14 | 15 | 15 | 16 | x | S |
学校决定派乙运动员参加比赛，理由是 ．
