题目内容
【题目】综合与实践:
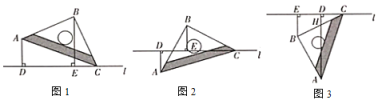
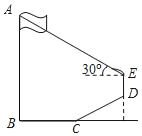
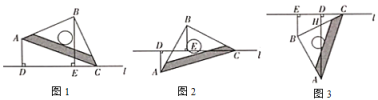
如图1,将一个等腰直角三角尺![]() 的顶点
的顶点![]() 放置在直线
放置在直线![]() 上,
上,![]() ,
,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() .
.
观察发现:
(1)如图1.当![]() ,
,![]() 两点均在直线
两点均在直线![]() 的上方时,
的上方时,
①猜测线段![]() ,
,![]() 与
与![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
②直接写出线段![]() ,
,![]() 与
与![]() 的数量关系;
的数量关系;
操作证明:
(2)将等腰直角三角尺![]() 绕着点
绕着点![]() 逆时针旋转至图2位置时,线段
逆时针旋转至图2位置时,线段![]() ,
,![]() 与
与![]() 又有怎样的数量关系,请写出你的猜想,并写出证明过程;
又有怎样的数量关系,请写出你的猜想,并写出证明过程;
拓广探索:
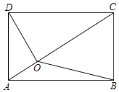
(3)将等腰直角三用尺![]() 绕着点
绕着点![]() 继续旋转至图3位置时,
继续旋转至图3位置时,![]() 与
与![]() 交于点
交于点![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长度.
的长度.
【答案】(1)①![]() . 理由见解析;②
. 理由见解析;②![]() ;(2)
;(2)![]() ;证明见解析;(3)
;证明见解析;(3)![]() 的长度为
的长度为![]() .
.
【解析】
(1)过点![]() 作
作![]() 根据已知条件结合直角三角形性质证明
根据已知条件结合直角三角形性质证明![]() ,从而得到四边形
,从而得到四边形![]() 为正方形,最后得出①
为正方形,最后得出①![]() ,直接写出②
,直接写出②![]() (2)过点
(2)过点![]() 作
作![]() ,先证明
,先证明![]() 证明四边形
证明四边形![]() 为正方形,根据正方形的性质求解(3)过点
为正方形,根据正方形的性质求解(3)过点![]() 作
作![]() ,证明
,证明![]() ,四边形
,四边形![]() 为正方形,再求解.
为正方形,再求解.
解:(1)①![]() .
.
理由如下:
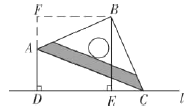
如图,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
又∵![]()
∴![]()
∴四边形![]() 为矩形.
为矩形.
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
即![]() .
.
在![]() 和
和![]() 中,
中,
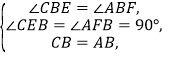
∴![]() .
.
∴![]() ,
,![]() .
.
又∵四边形![]() 为矩形,
为矩形,
∴四边形![]() 为正方形.
为正方形.
∴![]() .
.
∴![]() .
.
②![]() .
.
(2)
如图,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴四边形![]() 为矩形.
为矩形.
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
∴![]() .
.
∴![]() ,
,![]() .
.
又∵四边形![]() 为矩形,
为矩形,
∴四边形![]() 为正方形.
为正方形.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
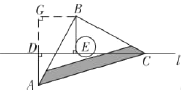
(3)
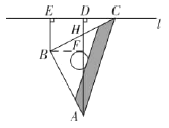
如图,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
同理可证,![]() ,四边形
,四边形![]() 为正方形.
为正方形.
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】某校初一年级68名师生参加社会实践活动,计划租车前往,租车收费标准如下:
车型 | 大巴车 (最多可坐55人) | 中巴车 (最多可坐39人) | 小巴车 (最多可坐26人) |
每车租金 (元∕天) | 900 | 800 | 550 |
则租车一天的最低费用为____元.