题目内容
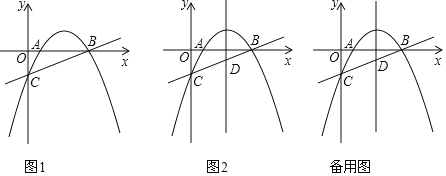
【题目】如图,直线![]() 与x轴、y轴分别交于BC两点,抛物线
与x轴、y轴分别交于BC两点,抛物线![]() 经过B、C两点,且与x轴交于点A
经过B、C两点,且与x轴交于点A
(1)求该抛物线的函数表达式;
(2)已知点M是第一象限内抛物线上的一个动点,过点M作MN平行于y轴交直线BC于点N,连接AM、BM、AN,求四边形MANB面积S的最大值,并求出此时点M的坐标;
(3)抛物线的对称轴交直线BC于点D,若Q为y轴上一点,则在抛物线上是否存在一点P,使得以B、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)当t=
;(2)当t=![]() 时,S四边形MANB的最大值=5,此时点M
时,S四边形MANB的最大值=5,此时点M![]() ;(3)P坐标为
;(3)P坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)直线![]() 与x轴、y轴的交点为B(5,0),C(0,﹣2),代入抛物线解析式可求出a,c的值;
与x轴、y轴的交点为B(5,0),C(0,﹣2),代入抛物线解析式可求出a,c的值;
(2)设点![]() ,用含t的代数式表示四边形MANB的面积,得到S与t的函数关系式,利用二次函数最大值求出t的值;
,用含t的代数式表示四边形MANB的面积,得到S与t的函数关系式,利用二次函数最大值求出t的值;
(3)存在,分BD为平行四边形的边或对角线进行分类讨论.
解:(1)由![]() x﹣2=0得x=5,
x﹣2=0得x=5,
∴B(5,0),令x=0,得y=﹣2,
∴C(0,﹣2),
由题意得:![]() ,
,
解得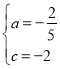 ,
,
∴抛物线解析式为 ![]() .
.
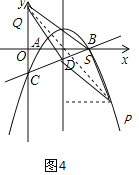
(2)如图1,设![]() ,
,
![]()
S四边形MANB=S△AMN+S△BMN
=![]() AGMN+
AGMN+![]() BGMN
BGMN
=![]() MN(AG+BG)
MN(AG+BG)
=![]() MNAB
MNAB
=![]() ×4(
×4(![]() t2+2t)
t2+2t)
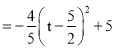
∵![]() <0,
<0,
∴当t=![]() 时,S四边形MANB的最大值=5,此时点M
时,S四边形MANB的最大值=5,此时点M![]() .
.
(3)存在.由为 ![]() ,
,
∴抛物线对称轴x=3.对称轴交x轴于F,
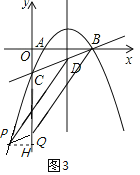
①以BD为边,PQ在BC上方,如图2,D(3,![]() ),F(3,0),
),F(3,0),
∵四边形BDQP是平行四边形,∴BD∥PQ,BD=PQ,
过点P作PH⊥y轴于H,
∴∠PHQ=∠BFD=90°,∠PQH=∠BCO=∠BDF,
∴△PQH≌△BDF,
∴PH=BF=2,HQ=FD=![]() ,
,
∴P(2,![]() ).
).
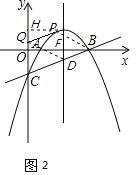
②以BD为边,PQ在BC下方,如图3,仿照①可求得P![]() ,
,
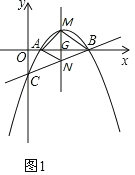
③以BD为平行四边形对角线,如图4,设BD中点为S,则S![]() ,
,
∵BPDQ是平行四边形,
∴BD与PQ互相平分,
∴SQ=SP,
∴S是PQ中点,
设![]() ,
,
∴![]() ,
,
∴a=8,
∴P(8,![]() )
)
综上所述,P坐标为![]() 或
或![]() 或
或![]() .
.