ЬтФПФкШн
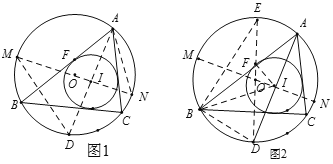
ЁОЬтФПЁПЖўДЮКЏЪ§ЭМЯѓЪЧХзЮяЯпЃЌХзЮяЯпЪЧжИЦНУцФкЕНвЛИіЖЈЕу![]() КЭвЛЬѕЖЈжБЯп
КЭвЛЬѕЖЈжБЯп![]() ОрРыЯрЕШЕФЕуЕФЙьМЃЃЎЦфжаЖЈЕу
ОрРыЯрЕШЕФЕуЕФЙьМЃЃЎЦфжаЖЈЕу![]() НаХзЮяЯпЕФНЙЕуЃЌЖЈжБЯп
НаХзЮяЯпЕФНЙЕуЃЌЖЈжБЯп![]() НаХзЮяЯпЕФзМЯпЃЎ
НаХзЮяЯпЕФзМЯпЃЎ
ЂйХзЮяЯп![]() (
(![]() )ЕФНЙЕуЮЊ
)ЕФНЙЕуЮЊ![]() ЃЌР§ШчЃЌХзЮяЯп
ЃЌР§ШчЃЌХзЮяЯп![]() ЕФНЙЕуЪЧ
ЕФНЙЕуЪЧ![]() ЃЛХзЮяЯп
ЃЛХзЮяЯп![]() ЕФНЙЕуЪЧ___________ЃЛ
ЕФНЙЕуЪЧ___________ЃЛ
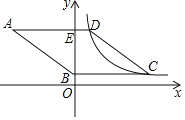
ЂкНЋХзЮяЯп![]() (
(![]() )ЯђгвЦНвЦ
)ЯђгвЦНвЦ![]() ИіЕЅЮЛЁЂдйЯђЩЯЦНвЦ
ИіЕЅЮЛЁЂдйЯђЩЯЦНвЦ![]() ИіЕЅЮЛ(
ИіЕЅЮЛ(![]() ЃЌ
ЃЌ![]() )ЃЌПЩЕУХзЮяЯп
)ЃЌПЩЕУХзЮяЯп![]() ЃЛвђДЫХзЮяЯп
ЃЛвђДЫХзЮяЯп![]() ЕФНЙЕуЪЧ
ЕФНЙЕуЪЧ![]() ЃЎР§ШчЃЌХзЮяЯп
ЃЎР§ШчЃЌХзЮяЯп![]() ЕФНЙЕуЪЧ
ЕФНЙЕуЪЧ![]() ЃЛХзЮяЯп
ЃЛХзЮяЯп![]() ЕФНЙЕуЪЧ_____________________ЃЎИљОнвдЩЯВФСЯНтОіЯТСаЮЪЬтЃК
ЕФНЙЕуЪЧ_____________________ЃЎИљОнвдЩЯВФСЯНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЭъГЩЬтжаЕФЬюПеЃЛ
ЃЈ2ЃЉвбжЊЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
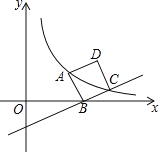
ЂйЧѓЦфЭМЯѓЕФНЙЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЂкЧѓЙ§Еу![]() Чвгы
Чвгы![]() жсЦНааЕФжБЯпгыЖўДЮКЏЪ§
жсЦНааЕФжБЯпгыЖўДЮКЏЪ§![]() ЭМЯѓНЛЕуЕФзјБъЃЎ
ЭМЯѓНЛЕуЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЃЈ2ЃЉЂй
ЃЛЃЈ2ЃЉЂй![]() ЃЛЂк
ЃЛЂк![]() КЭ
КЭ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉжБНгИљОнаТЖЈвхМДПЩЧѓГіХзЮяЯпЕФНЙЕуЃЛ
ЃЈ2ЃЉЂйЯШНЋЖўДЮКЏЪ§НтЮіЪНХфГЩЖЅЕуЪНЃЌдйИљОнаТЖЈвхМДПЩЧѓГіХзЮяЯпЕФНЙЕуЃЛ
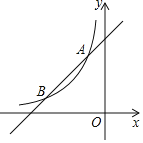
ЂквРЬтвтПЩЕУЕу![]() Чвгы
Чвгы![]() жсЦНааЕФжБЯпЃЌИљОнЦНаагкxжсЕФжБЯпЩЯЕФЕуЕФзнзјБъЯрЕШЃЌНЋЕуFЕФзнзјБъДњШыНтЮіЪНМДПЩЧѓЕУxЕФжЕЃЌДгЖјЕУГіНЛЕузјБъЃЎ
жсЦНааЕФжБЯпЃЌИљОнЦНаагкxжсЕФжБЯпЩЯЕФЕуЕФзнзјБъЯрЕШЃЌНЋЕуFЕФзнзјБъДњШыНтЮіЪНМДПЩЧѓЕУxЕФжЕЃЌДгЖјЕУГіНЛЕузјБъЃЎ
ЃЈ1ЃЉЂйИљОнаТЖЈвхЃЌПЩЕУ![]() ЃЌ
ЃЌ
ЫљвдХзЮяЯп![]() ЕФНЙЕуЪЧ
ЕФНЙЕуЪЧ![]() ЃЛ
ЃЛ
ЂкИљОнаТЖЈвхЃЌПЩЕУh=1ЃЌ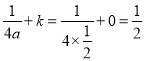 ЃЌ
ЃЌ
ЫљвдХзЮяЯп![]() ЕФНЙЕуЪЧ
ЕФНЙЕуЪЧ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйНЋ![]() ЛЏЮЊЖЅЕуЪНЕУЃК
ЛЏЮЊЖЅЕуЪНЕУЃК
![]()
ИљОнаТЖЈвхЃЌПЩЕУh=1ЃЌ![]() ЃЌ
ЃЌ
ЫљвдПЩЕУХзЮяЯп![]() ЕФНЙЕузјБъ
ЕФНЙЕузјБъ![]() ЃЛ
ЃЛ
ЂкгЩЂйжЊ![]() ЃЌЫљвдЙ§Еу
ЃЌЫљвдЙ§Еу![]() Чвгы
Чвгы![]() жсЦНааЕФжБЯпЪЧ
жсЦНааЕФжБЯпЪЧ![]() ЃЌ
ЃЌ
НЋ![]() ДњШы
ДњШы![]() ЕУЃК
ЕУЃК
![]() ЃЌ
ЃЌ
НтЕУЃК![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЫљвдЃЌЙ§Еу![]() Чвгы
Чвгы![]() жсЦНааЕФжБЯпгыЖўДЮКЏЪ§
жсЦНааЕФжБЯпгыЖўДЮКЏЪ§![]() ЭМЯѓНЛЕуЕФзјБъЮЊ
ЭМЯѓНЛЕуЕФзјБъЮЊ![]() КЭ
КЭ![]() ЃЎ
ЃЎ