Question

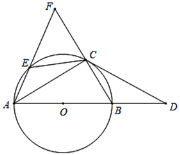
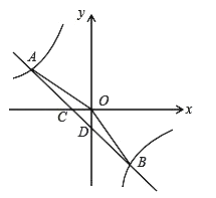
【题目】如图，点A，P，B，C是⊙O上的四个点，∠DAP＝∠PBA．

（1）求证：AD是⊙O的切线；

（2）若∠APC＝∠BPC＝60°，试探究线段PA，PB，PC之间的数量关系，并证明你的结论；

（3）在第（2）问的条件下，若AD＝2，PD＝1，求线段AC的长．

Answer 1

【答案】（1）证明见解析；（2）PA+PB＝PF+FC＝PC；（3）1+．

【解析】

（1）欲证明AD是⊙O的切线，只需推知AD⊥AE即可；

（2）首先在线段PC上截取PF=PB，连接BF，进而得出△BPA≌△BFC（AAS），即可得出PA+PB=PF+FC=PC；

（3）利用△ADP∽△BDA，得出＝＝，求出BP的长，进而得出△ADP∽△CAP，则＝，则AP2=CPPD求出AP的长，即可得出答案．

（1）证明：先作⊙O的直径AE，连接PE，

∵AE是直径，

∴∠APE＝90°．

∴∠E+∠PAE＝90°．

又∵∠DAP＝∠PBA，∠E＝∠PBA，

∴∠DAP＝E，

∴∠DAP+∠PAE＝90°，即AD⊥AE，

∴AD是⊙O的切线；

（2）PA+PB＝PC，

证明：在线段PC上截取PF＝PB，连接BF，

∵PF＝PB，∠BPC＝60°，

∴△PBF是等边三角形，

∴PB＝BF，∠BFP＝60°，

∴∠BFC＝180°﹣∠PFB＝120°，

∵∠BPA＝∠APC+∠BPC＝120°，

∴∠BPA＝∠BFC，

在△BPA和△BFC中，

，

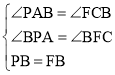∴△BPA≌△BFC（AAS），

∴PA＝FC，AB＝CB，

∴PA+PB＝PF+FC＝PC；

（3）∵△ADP∽△BDA，

∴＝＝，

∵AD＝2，PD＝1，

∴BD＝4，AB＝2AP，

∴BP＝BD﹣DP＝3，

∵∠APD＝180°﹣∠BPA＝60°，

∴∠APD＝∠APC，

∵∠PAD＝∠E，∠PCA＝∠E，

∴∠PAD＝∠PCA，

∴△ADP∽△CAP，

∴＝，

∴AP2＝CPPD，

∴AP2＝（3+AP）1，

解得：AP＝或AP＝（舍去），

由(2)知△ABC是等边三角形，

∴AC=BC＝AB＝2AP＝1+．