题目内容
如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点,以OA为半径的⊙O经过点D。求证:BC是⊙O切线.


证明见解析.
试题分析:如图,连接OD.欲证BC是⊙O切线,只需证明OD⊥BC即可.
如图,连接OD.设AB与⊙O交于点E.

∵AD是∠BAC的平分线,
∴∠BAC=2∠BAD,
又∵∠EOD=2∠EAD,
∴∠EOD=∠BAC,
∴OD∥AC.
∵∠ACB=90°,
∴∠BDO=90°,即OD⊥BC,
又∵OD是⊙O的半径,
∴BC是⊙O切线.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
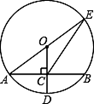
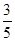 ,求⊙O的半径.
,求⊙O的半径.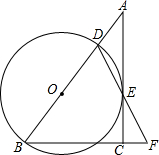
 ,则CN的长为 .
,则CN的长为 .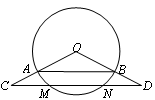
 的值为( )
的值为( )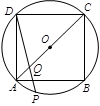


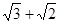

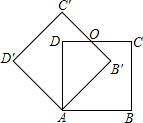
 ,则在旋转过程中点D到D’的路径长是
,则在旋转过程中点D到D’的路径长是