题目内容
已知⊙O的半径为12cm，弦AB=16cm．
（1）求圆心O到弦AB的距离；
（2）如果弦AB的长度保持不变，两个端点在圆周上滑动，那么弦AB的中点形成什么样的图形？
（1）求圆心O到弦AB的距离；
（2）如果弦AB的长度保持不变，两个端点在圆周上滑动，那么弦AB的中点形成什么样的图形？
（1）圆心O到弦AB的距离是
cm；
（2）弦AB的中点形成一个以O为圆心，以cm为半径的圆周．
cm；（2）弦AB的中点形成一个以O为圆心，以
cm为半径的圆周．试题分析：（1）连接OB，过O作OC⊥AB于C，则线段OC的长就是圆心O到弦AB的距离，求出BC，再根据勾股定理求出OC即可；
（2）弦AB的中点形成一个以O为圆心，以4
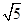cm为半径的圆周．（1）如图，连接OB，过O作OC⊥AB于C，则线段OC的长就是圆心O到弦AB的距离，
∵OC⊥AB，OC过圆心O，
∴AC=BC=
AB=8cm，在Rt△OCB中，由勾股定理得：
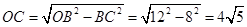（cm），答：圆心O到弦AB的距离是
cm．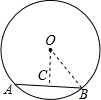
（2）解：如果弦AB的长度保持不变，两个端点在圆周上滑动，那么弦AB的中点到圆心O的距离都是
cm，∴如果弦AB的长度保持不变，两个端点在圆周上滑动，那么弦AB的中点形成一个以O为圆心，以
cm为半径的圆周．
练习册系列答案
相关题目
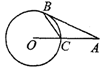
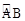上两点，AB＝13，AC＝5，
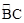的中点，求PA得长 .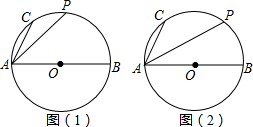
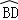的中点，连接AE交BC于点F，当BD=5，CD=4时，求AF的值．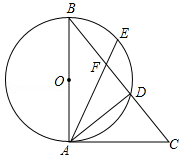
度数为60 o，∠BOE＝45o，DA⊥OB，EB⊥OB．
的值；
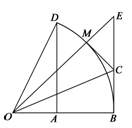
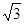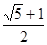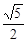a
a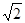
a
a