题目内容
如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC．
求证：EF是⊙O的切线。
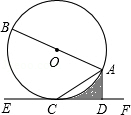
求证：EF是⊙O的切线。
证明见解析．
试题分析：连接OC，由OA=OC，利用等边对等角得到∠OAC=∠OCA，由∠DAC=∠BAC，等量代换得到一对内错角相等，得到AD与OC平行，由AD垂直于EF，得到OC垂直于EF，即可得到EF为圆O的切线；
连接OC，
∵OA=OC，
∴∠OAC=∠OCA，
∵∠DAC=∠BAC，
∴∠DAC=∠OCA，
∴AD∥OC，
∵AD⊥EF，
∴OC⊥EF，
则EF为圆O的切线
练习册系列答案
相关题目
，求DE的长．
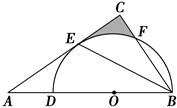
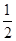，⊙O的半径为4，求图中阴影部分的面积．
,母线长是6 cm,则该圆锥的侧面展开图的圆心角的度数是 ．
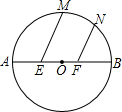
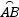上两点，且∠MEB=∠NFB=60°，则EM+FN= ．