题目内容
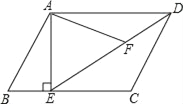
【题目】如图,平行四边形ABCD,AE⊥BC交点E,连接DE,F为DE上一点,且∠AFE=∠B=60°.
(1)求证:△ADF∽△DEC;
(2)若AE=3,AD=4,求EF的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由平行四边形的性质结合等角的补角相等,可得出∠AFD=∠C=120°、AD∥BC,利用平行线的性质可得出∠ADF=∠DEC,进而即可证出△ADF∽△DEC;
(2)由AE及∠B的值可求出BE、CE的长度,在Rt△ADE中,利用勾股定理可求出DE的长度,由△ADF∽△DEC利用相似三角形的性质即可求出DF的长度,再将其代入EF=DE-DF中即可求出EF的长.
(1)证明:∵四边形ABCD为平行四边形,∠AFE=∠B=60°,
∴∠AFD=∠C=120°,AD∥BC,
∴∠ADF=∠DEC,
∴△ADF∽△DEC.
(2)解:∵AE=3,∠B=60°,
∴BE=![]() ,CE=4﹣
,CE=4﹣![]() .
.
在Rt△ADE中,AE=3,AD=4,
∴DE=![]() =5.
=5.
∵△ADF∽△DEC,
∴![]() ,即
,即![]() ,
,
∴DF=![]() ,
,
∴EF=DE﹣DF=![]() .
.

练习册系列答案
相关题目