Question

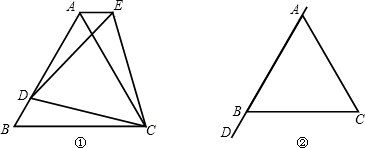
如图①，M、N点分别在等边三角形的BC、CA边上，且BM=CN，AM、BN交于点Q．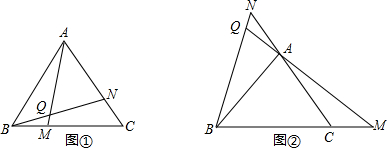
（1）求证：∠BQM=60°；
（2）如图②，如果点M、N分别移动到BC、CA的延长线上，其它条件不变，（1）中的结论是否仍然成立？若成立，给予证明；若不成立，说明理由．

Answer 1

（1）证明：∵△ABC为等边三角形，
∴AB=BC，∠ABC=∠C=60°，
在△ABM和△BCN中

AB=BC ∠ABM=∠C BM=CN

，
∴△ABM≌△BCN，
∴∠BAM=∠CBN，
∵∠BQM=∠ABQ+∠BAQ，
∴∠BQM=∠ABQ+∠QBM=∠ABM=60°；

（2）（1）中的结论仍然成立．理由如下：
与（1）的证明方法一样可证明△ABM≌△BCN，
∴∠M=∠N，
∵∠BQA=∠N+∠NAQ，∠BCA=∠M+∠CAM，
而∠NAQ=∠CAM，
∴∠BQA=∠BCA=60°，
即∠BQM=60°．