题目内容
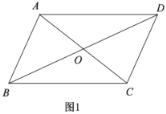
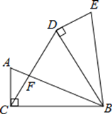
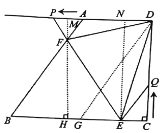
【题目】如图,在四边形![]() 中,
中,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() 同时,点
同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连
,连![]() 接,交
接,交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() .解答下列问题:
.解答下列问题:
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设五边形![]() 的面积为
的面积为![]() , 求
, 求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)连接![]() .是否存在某一时刻
.是否存在某一时刻![]() , 使点
, 使点![]() 在
在![]() 的垂直平分线上,若存在,求出的值;若不存在,说明理由.
的垂直平分线上,若存在,求出的值;若不存在,说明理由.
【答案】(1)当![]() 为
为![]() 时,2
时,2![]() ;(2)
;(2)![]() ;(3)存在,当
;(3)存在,当![]() 为
为![]() 时,点
时,点![]() 在
在![]() 的垂直平分线上.
的垂直平分线上.
【解析】
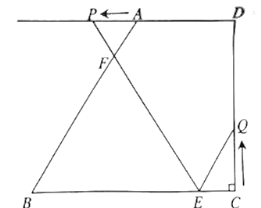
(1)如图1,作辅助线,构建平行线,证明QE∥DG,得![]() ,则
,则![]() ,得EC=3t,由BE=2EC解方程可得t的值;
,得EC=3t,由BE=2EC解方程可得t的值;
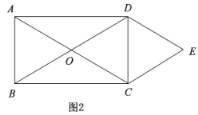
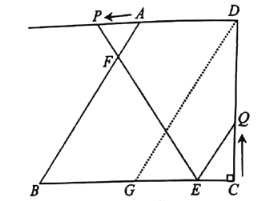
(2)如图2,作辅助线,构建两个三角形的高线FM,FH,先证明四边形MHCD是矩形,得MH=CD=8,HM⊥AD,证明△APF∽△BEF,列比例式可得HF=8-2t,最后利用面积差可得:y=S四边形ABCD-S△EFB-S△ECQ,代入面积公式可得结论;
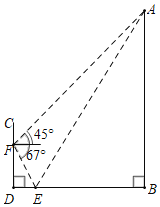
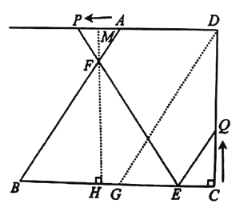
(3)如图3,作辅助线,构建直角三角形,表示各边的长,利用勾股定理计算PE=10,PN=6,由△APF∽△BEF,得![]() ,表示PF和EF的长,利用勾股定理计算PM、MD的长,若点F在DE的垂直平分线上,则FE=FD,列方程可得t的值.
,表示PF和EF的长,利用勾股定理计算PM、MD的长,若点F在DE的垂直平分线上,则FE=FD,列方程可得t的值.
![]() 过点
过点![]() 作
作![]() ,交
,交![]() 于点
于点![]()
![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
解得:![]()
![]() 当
当![]() 为
为![]() 时,2
时,2![]()
![]() 过点
过点![]() 作
作![]() ,交
,交![]() 为
为![]() ,交
,交![]() 为
为![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 与
与![]() 的函数关系式是
的函数关系式是![]()
![]() 过点
过点![]() 作
作![]() 垂足为
垂足为![]() ,则
,则![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
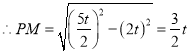
![]()

若点![]() 在
在![]() 的垂直平分线上
的垂直平分线上
则![]() 时,
时,![]()
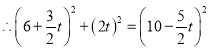
![]()
![]()
![]() 当
当![]() 为
为![]() 时,点
时,点![]() 在
在![]() 的垂直平分线上。
的垂直平分线上。

【题目】为了抗击新冠病毒疫情,全国人民众志成城,守望相助.春节后某地一水果购销商安排15辆汽车装运A,B,C三种水果120吨销售,所得利润全部捐赠湖北抗疫.已知按计划15辆汽车都要装满且每辆汽车只能装同一种水果,每种水果所用车辆均不少于3辆,汽车对不同水果的运载量和每吨水果销售获利情况如下表.
水果品种 | A | B | C |
汽车运载量(吨/辆) | 10 | 8 | 6 |
水果获利(元/吨) | 800 | 1200 | 1000 |
(1)设装运A种水果的车辆数为x辆,装运B种水果车辆数为y辆,根据上表提供的信
息,
①求y与x之间的函数关系式;
②设计车辆的安排方案,并写出每种安排方案;
(2)若原有获利不变的情况下,当地政府按每吨50元的标准实行运费补贴,该经销商打算将获利连同补贴全部捐出.问应采用哪种车辆安排方案,可以使这次捐款数w(元)最大化?捐款w(元)最大是多少?