题目内容
【题目】已知：四边形
中，对角线
、
相交于点
，
，
．
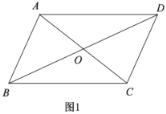
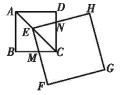
（1）如图1，求证：四边形为平行四边形；
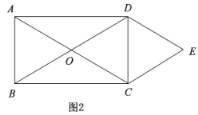
（2）如图2，
，
，
，
，
，求四边形
的面积．
【答案】（1）详见解析；（2）
【解析】
（1）根据平行线的性质可得
，然后利用ASA即可证出
，从而得出
，最后根据平行四边形的判定定理即可证出结论；
（2）根据矩形的判定定理可知四边形
是矩形，从而得出
，从而证出
是等边三角形，利用锐角三角函数求出CD，根据平行四边形的性质可得四边形
是平行四边形，作
于
，利用锐角三角函数求出DH，最后根据平行四边形的面积公式即可求出结论．
（1）证明：∵
∴
∵
，
∴
∴
∴四边形是平行四边形
（2）∵
∴四边形是矩形
∴
与
相等且互相平分
∴
∵
∴
∴是等边三角形
∴
∵
，
∴
∵
，
∴四边形是平行四边形
作于
∵
∴
∴
练习册系列答案
培优口算题卡系列答案
相关题目
