题目内容
【题目】如图(1),在矩形ABCD中,AB=3,BC=4,连接BD.现将一个足够大的直角三角板的直角顶点P放在BD所在的直线上,一条直角边过点C,另一条直角边与AB所在的直线交于点G.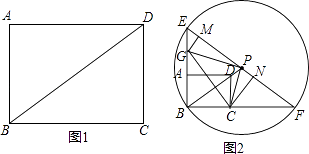
(1)是否存在这样的点P,使点P、C、G为顶点的三角形与△GCB全等?若存在,画出图形,并直接在图形下方写出BG的长.(如果你有多种情况,请用①、②、③、…表示,每种情况用一个图形单独表示,如果图形不够用,请自己画图)
(2)如图(2),当点P在BD的延长线上时,以P为圆心、PB为半径作圆分别交BA、BC延长线于点E、F,连EF,分别过点G、C作GM⊥EF,CN⊥EF,M、N为垂足.试探究PM与FN的关系.
【答案】
(1)解:存在点P,使点P、C、G为顶点的三角形与△GCB全等.
①若点G在线段AB上,如图①.
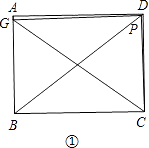
当BG=PC时,根据HL可得Rt△GBC≌Rt△CPG,
此时∠GCB=∠CGP,
∴PG∥BC,
∴∠GPC+∠PCB=90°.
∵∠GPC=90°,
∴∠PCB=90°,
∴点P在点D处,
∴BG=PC=DC=AB=3;
②若点G在线段AB的延长线上,如图②.
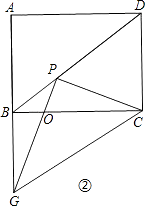
当BG=PC时,根据HL可得Rt△GBC≌Rt△CPG,
此时BC=PG,∠GCB=∠CGP,
∴OG=OC,OB=OP,
∴∠PBO=∠BPO= ![]() (180°﹣∠BOP),
(180°﹣∠BOP),
∠OCG=∠OGC= ![]() (180°﹣∠GOC).
(180°﹣∠GOC).
∵∠BOP=∠GOC,
∴∠PBO=∠OCG,
∴BD∥CG.
∵四边形ABCD是矩形,
∴AB∥DC,即BG∥DC,
∴四边形BGCD是平行四边形,
∴BG=CD=3;
③若点G在线段AB的反向延长线上,如图③.
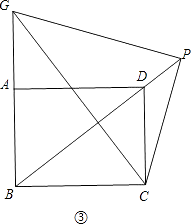
当PC=BC时,根据HL可得Rt△GBC≌Rt△GPC,
此时BG=PG,
∴点G、C在BP的垂直平分线上,
∴GC垂直平分BP,
∴∠BGC+∠GBD=90°.
∵∠CBD+∠GBD=90°,
∴∠BGC=∠CBD.
又∵∠GBC=∠BCD=90°,
∴△GCB∽△BDC,
∴ ![]() .
.
∵BC=4,CD=3,
∴ ![]() =
= ![]() ,
,
∴BG= ![]() ;
;
(2)解:如图2,
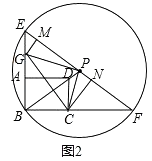
由(1)可知,此时△GBC≌△GPC,且BG=PG= ![]() ,BC=PC=4.
,BC=PC=4.
∵GM⊥EF,CN⊥EF,
∴∠GMP=∠PNC=90°,
∴∠MGP+∠GPM=90°.
∵∠GPC=90°,
∴∠GPM+∠NPC=90°,
∴∠MGP=∠NPC,
∴△PGM∽△CPN,
∴ ![]() .
.
∴ ![]() =
= ![]() ,即PM=
,即PM= ![]() CN.
CN.
∵PB=PF,∴∠F=∠PBC.
又∵∠FNC=∠BCD=90°,
∴△FNC∽△BCD,
∴ ![]() .
.
∵BC=4,DC=3,
∴ ![]() ,
,
∴FN= ![]() CN,
CN,
∴PM=FN.
【解析】(1)当BG=PC时,根据HL可得Rt△GBC≌Rt△CPG,此时∠GCB=∠CGP,得到PG∥BC,∠GPC+∠PCB=90°;由∠GPC=90°,∠PCB=90°,点P在点D处,得到BG=PC=DC=AB=3;(2)由(1)可知,此时△GBC≌△GPC,知道BG=PG,BC=PC的值,根据两角对应相等两三角形相似,得到△PGM∽△CPN,得到比例,得到△FNC∽△BCD,得到比例,得到PM=FN.
【考点精析】认真审题,首先需要了解圆心角、弧、弦的关系(在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.