题目内容
【题目】如图,在矩形ABCD中,点O是对角线AC上一点,以OC为半径的⊙O与CD交于点M,且∠BAC=∠DAM.
(1)求证:AM与⊙O相切;
(2)若AM=3DM,BC=2,求⊙O的半径.
【答案】
(1)证明:连接OM. 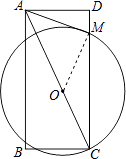
在矩形ABCD中,AB∥DC,∠D=90°
∴∠BAC=∠DCA,
∵OM=OC,
∴∠OMC=∠OCM.
∵∠BAC=∠DAM,
∴∠DAM=∠OMC.
∴∠OMC+∠DMA=∠DAM+∠DMA.
在△DAM中,∠D=90°,
∴∠DAM+∠DMA=180°﹣90°=90°.
∴∠OMC+∠DMA=90°.
∴∠AMO=90°,
∴AM⊥MO.
点M在⊙O上,OM是⊙O的半径,
∴AM与⊙O相切.
(2)在△BAC与△DAM中,
∵∠BAC=∠DAM,∠B=∠D,
∴△BAC∽△DAM,
∴ ![]() ,
,
∴ ![]() .
.
∵AM=3DM,
∴AC=3BC.BC=2,
∴AC=6,
在△DAM中,DM2+AD2=AM2
即DM2+22=(3DM)2
解得DM= ![]() .AM=
.AM= ![]() .
.
在△AMO中,AM2+MO2=AO2
即( ![]() )2+MO2=(6﹣MO)2.
)2+MO2=(6﹣MO)2.
解得MO= ![]() .
.
【解析】(1)根据矩形的性质和等边对等角得到AM⊥MO,由点M在⊙O上,OM是⊙O的半径,得到AM与⊙O相切;(2)根据两角相等两三角形相似,得到△BAC∽△DAM,得到比例,求出AC的值,在△DAM中,根据勾股定理求出MO的值.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目