题目内容
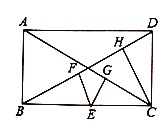
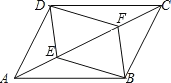
【题目】已知:如图,E、F是口ABCD的对角线AC上的两点,且AF=CE.
⑴求证:△CDF≌△ABE;
⑵求证:ED∥BF.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据已知条件得到AE=CF,根据平行四边形的性质得到∠DCF=∠BAE,根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质得到BE=DF,∠AEB=∠CFD,根据平行四边形的判定和性质即可得到结论.
(1)证明:∵AF=CE,
∴AF-EF=CE-EF,
即AE=CF,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠DCF=∠BAE,
在△CDF与△ABE中,
 ,
,
∴△CDF≌△ABE(SAS);
(2)∵△ABE≌△CDF,
∴BE=DF,∠AEB=∠CFD,
∴∠BEF=∠DFE,
∴BE∥DF,
∴四边形DEBF是平行四边形,
∴ED∥BF.

练习册系列答案
相关题目