题目内容
（1）化简求值：(| x2-2x-3 |
| x2-1 |
| x-3 |
| x-1 |
（2）在△ABC中，AB=13，BC=14，AC=15，求BC边上的高AD．
分析：（1）对括号里的分式因式分解，再把除法转化成乘法进行计算，最后把x的值代入计算即可；
（2）先设BD=x，由于AD是高，可得两个直角三角形，分别在每一个直角三角形中利用勾股定理求出AD2，列出等式，解出x，再利用勾股定理即可求AD．
（2）先设BD=x，由于AD是高，可得两个直角三角形，分别在每一个直角三角形中利用勾股定理求出AD2，列出等式，解出x，再利用勾股定理即可求AD．
解答：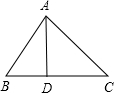
（1）解：原式=
×
=1，
当x=2时，原式=1；
（2）如右图所示，
设BD=x，则CD=14-x，
∵AD⊥BC，
∴∠ADB=∠ADC=90°，
在Rt△ABD中，AD2=AB2-x2，
同理有AD2=AC2-（14-x）2，
∴132-x2=152-（14-x）2，
解得x=5，
∴AD=
=12．
（1）解：原式=| (x+1)(x-3) |
| (x+1)(x-1) |
| x-1 |
| x-3 |
当x=2时，原式=1；
（2）如右图所示，
设BD=x，则CD=14-x，
∵AD⊥BC，
∴∠ADB=∠ADC=90°，
在Rt△ABD中，AD2=AB2-x2，
同理有AD2=AC2-（14-x）2，
∴132-x2=152-（14-x）2，
解得x=5，
∴AD=
| 132-52 |
点评：本题考查了分式的化简求值、勾股定理．解题的关键是先把分式化成最简；在两个直角三角形中分别表示AD，找出等量关系，求出x．
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目