题目内容
【题目】在正方形![]() 中,
中,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() ,
,![]() 上,且
上,且![]() 垂直
垂直![]() .
.
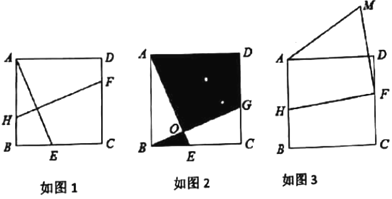
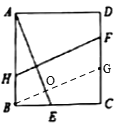
(1)如图1,求证:![]() ;
;
(2)如图2,平移线段![]() 至线段
至线段![]() ,
,![]() 交
交![]() 于点
于点![]() ,图中阴影部分的面积与正方形的面积之比为
,图中阴影部分的面积与正方形的面积之比为![]() ,求
,求![]() 的周长;
的周长;
(3)如图3,若![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至线段
至线段![]() ,连接
,连接![]() ,则线段
,则线段![]() 的最小值为______.
的最小值为______.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,利用直角三角形两锐角互余的关系可得
,利用直角三角形两锐角互余的关系可得![]() ,利用ASA可证明
,利用ASA可证明![]() ,根据全等三角形的性质即可得结论;(2)根据阴影部分的面积与正方形
,根据全等三角形的性质即可得结论;(2)根据阴影部分的面积与正方形![]() 的面积之比为
的面积之比为![]() 可求出空白部分的面积,根据
可求出空白部分的面积,根据![]() 可求出△ABO的面积,设
可求出△ABO的面积,设![]() ,
,![]() ,可得ab=4,根据勾股定理可得a2+b2=16,即可求出a+b=
,可得ab=4,根据勾股定理可得a2+b2=16,即可求出a+b=![]() ,进而可求出△ABO的周长;(3)过点
,进而可求出△ABO的周长;(3)过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,过B作BP//HF,交CD于P,可证明四边形
,过B作BP//HF,交CD于P,可证明四边形![]() 是平行四边形,可得
是平行四边形,可得![]() ,设
,设![]() ,分别用a表示出CN和CF的长,根据勾股定理表示出NF的长,利用二次函数的性质求出最小值即可.
,分别用a表示出CN和CF的长,根据勾股定理表示出NF的长,利用二次函数的性质求出最小值即可.
(1)如图,过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,
∵四边形ABCD是正方形,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,
上,
∴BH//GF,![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
∵![]() 垂直
垂直![]() ,HF//BG,
,HF//BG,
∴![]() 垂直
垂直![]() ,
,
∴![]() ,
,
∵∠ABE=![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,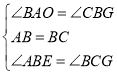 ,
,
∴![]() ,
,
∴![]() ,
,
∴AE=HF.
(2)∵阴影部分的面积与正方形![]() 的面积之比为
的面积之比为![]() ,
,
∴阴影部分的面积为![]() ,
,
∴空白部分的面积为![]() ,
,
由(1)得,![]() ,
,
∴![]() 的面积与四边形
的面积与四边形![]() 的面积相等,
的面积相等,
∴S△AOB=![]() ,
,
设![]() ,
,![]() ,则
,则![]() ,即
,即![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 的周长=AB+OA+OB=
的周长=AB+OA+OB=![]() .
.
(3)过点![]() 作
作![]() 的平行线交
的平行线交![]() 于点
于点![]() ,过B作BP//HF,交CD于P,
,过B作BP//HF,交CD于P,
∵![]() ,
,
∴![]() ,
,
由(1)得![]() ,△ABN≌△BCP,BH=PF,
,△ABN≌△BCP,BH=PF,
∴BN=CP,
∵![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
设![]() ,则
,则![]() ,CP=4-2a,
,CP=4-2a,
∴![]() ,
,
∴CN=4-BN=2a,
∴![]()
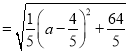 ,
,
∴当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目