题目内容
【题目】我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆．例如线段
的最小覆盖圆就是以线段为直径的圆．
（1）请分别作出图①中两个三角形的最小覆盖圆（要求用尺规作图，保留作图痕迹，不写作法）；
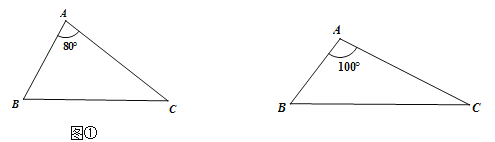
（2）三角形的最小覆盖圆有何规律？请直接写出你所得到的结论（不要求证明）；
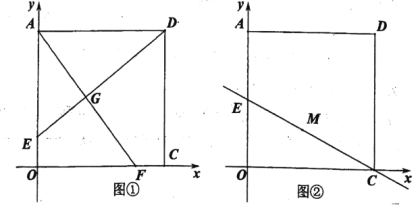
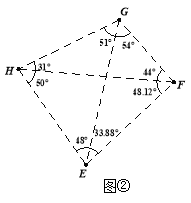
（3）某城市有四个小区
（其位置如图②所示），现拟建一个手机信号基站，为了使这四个小区居民的手机都能有信号，且使基站所需发射功率最小（距离越小，所需功率越小），此基站应建在何处？请写出你的结论并说明研究思路．
【答案】（1）图形见解析；（2）锐角三角形的最小覆盖圆是其外接圆，钝角三角形的最小覆盖圆是以其最长边为直径的圆，直角三角形的最小覆盖圆二者均可．（3）
的外接圆的圆心为手机信号基站所在位置．
【解析】
试题分析：（1）画出△ABC的外接圆即可；（2）锐角三角形的最小覆盖圆是其外接圆，钝角三角形的最小覆盖圆是以其最长边为直径的圆，直角三角形的最小覆盖圆二者均可．（3）的外接圆的圆心为手机信号基站所在位置．
试题解析：（1）如图所示：
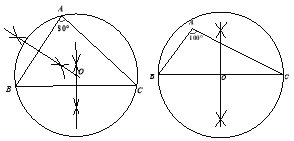
（2）锐角三角形的最小覆盖圆是其外接圆，钝角三角形的最小覆盖圆是以其最长边为直径的圆，直角三角形的最小覆盖圆二者均可．
（说明：写出三角形的最小覆盖圆是其外接圆，或是以其最长边为直径的圆，各给1分）
（3）结论：的外接圆的圆心为手机信号基站所在位置．
研究思路：
a．手机信号基站应建在四边形
的最小覆盖圆的圆心处；所以先考虑四边形的外接圆，因为对角不互补，所以该四边形没有外接圆；
b．作四边形对角线，将四边形分割成两个三角形，考虑其中一个三角形的最小覆盖圆能否覆盖另一个三角形，从而将四边形最小覆盖圆问题转化为三角形最小覆盖圆问题来研究；
c．若沿
分割，因为
，所以这两个三角形的最小覆盖圆均不能完全覆盖另一个三角形；
d．若沿
分割，因为
，所以存在一个三角形的最小覆盖圆能完全覆盖另一个三角形的情况，又因为
，所以的最小覆盖圆，即其外接圆能完全覆盖
，因此的外接圆的圆心为手机信号基站所在位置．
（说明：1．学生的答案只要涉及到将四边形问题转化为三角形问题，可以给第6分；
2．若学生答案含有以下情况之一，并借此分析沿分割和沿分割的差异性，均可以给第7分：
①比较四边形对角和的数量关系；
②同弧所对的圆周角的度数关系；
③画出四个三角形的最小覆盖圆，通过观察或测量，比较大小后发现的外接圆的圆心为手机信号站
所在位置．
3．重在判断学生思维的方向，不过多的要求语言的规范和思维的严谨．）
