题目内容
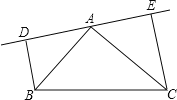
【题目】在一次数学课上，张老师出示了一个题目：“如图，ABCD的对角线相交于点O，过点O作EF垂直于BD交AB，CD分别于点F，E，连接DF，
请根据上述条件，写出一个正确结论
”其中四位同学写出的结论如下：
小青：
；小何：四边形DFBE是正方形；
小夏：
；小雨：
．
这四位同学写出的结论中不正确的是
A. 小青 B. 小何 C. 小夏 D. 小雨
【答案】B
【解析】
利用平行四边形的性质、全等三角形的判定和性质，一一判断即可．
∵四边形ABCD是平行四边形，
∴OA=OC，CD∥AB，
∴∠ECO=∠FAO，（故小雨的结论正确），
在△EOC和△FOA中，
∴△EOC≌△FOA，
∴OE=OF（故小青的结论正确），
∴S△EOC=S△AOF，
∴S四边形AFED=S△ADC=
S平行四边形ABCD，
∴S四边形AFED=S四边形FBCE故小夏的结论正确，
∵△EOC≌△FOA，
∴EC=AF，∵CD=AB，
∴DE=FB，DE∥FB，
∴四边形DFBE是平行四边形，
∵OD=OB，EO⊥DB，
∴ED=EB，
∴四边形DFBE是菱形，无法判断是正方形，故小何的结论错误，
故选：B
练习册系列答案
相关题目
