题目内容
如图,在△ABC中,EF∥BC,AE=2BE,则△AEF与梯形BCFE的面积比为________.

4:5
分析:先证△AEF∽△ABC,相似比是2:3,根据相似三角形性质,可求面积的比是4:9,故可求△AEF与梯形BCFE的面积比.
解答:解:AE=2BE,AB=3BE,则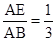 ,
,
根据EF∥BC,得到△AEF∽△ABC,相似比是2:3,
面积的比是相似比的平方,因而面积的比是4:9,
设△AEF的面积是4a,则△ABC的面积是9a,
则梯形BCFE的面积是5a,
因而△AEF与梯形BCFE的面积比4:5.
解答:解:AE=2BE,AB=3BE,则
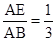 ,
,根据EF∥BC,得到△AEF∽△ABC,相似比是2:3,
面积的比是相似比的平方,因而面积的比是4:9,
设△AEF的面积是4a,则△ABC的面积是9a,
则梯形BCFE的面积是5a,
因而△AEF与梯形BCFE的面积比4:5.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目

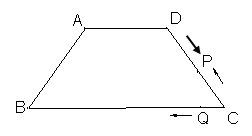
 中,
中, 、
、 分别为
分别为 、
、 边上的点,
边上的点, ∥
∥ ,
, 为
为 =5,
=5, =3,
=3, 的长为( )
的长为( )



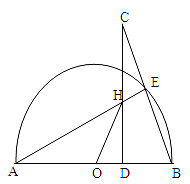
 △ABC中,
△ABC中,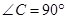 ,点
,点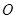 在
在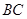 上,
上,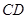 为⊙
为⊙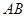 于
于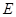 ,若
,若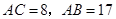 ,求⊙
,求⊙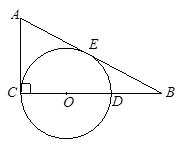
 (2)在图②中画一个与格点△ABC相似的格点△A2B2C2,且△A2B2C2与△ABC的相似比为2:1.
(2)在图②中画一个与格点△ABC相似的格点△A2B2C2,且△A2B2C2与△ABC的相似比为2:1.