题目内容
已知：等腰梯形ABCD，AD∥BC,AB=DC=5,AD=6,BC=12,动点P从点D出发沿DC以每秒1个单位向终点C运动，点Q从点C出发沿CB以每秒2个单位向B运动，当点P到达C时，点Q随之停止运动，设点P运动的时间为t秒.
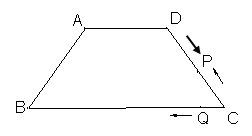
小题1:（1）求梯形ABCD面积.
小题2:（2）当PQ∥AB时，求t.
小题3:（3） 当点P、Q、C三点构RT△时，求t值.
小题1:（1）求梯形ABCD面积.
小题2:（2）当PQ∥AB时，求t.
小题3:（3） 当点P、Q、C三点构RT△时，求t值.
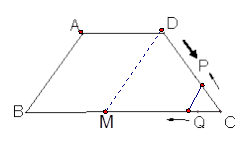
小题1:(1) 解：分别过点A，D作AE⊥BC，DF⊥BC，垂足分别为E，F
易证BE=CF，AD=EF
因为AB=DC=5,AD=6,BC=12
所以AE=DF=4
所以 梯形ABCD面积=36
小题2:(2)由题意知：CP="5-t," CQ=2t
如图，过点D作DM∥AB
∵PQ∥AB
∴ PQ∥DM BM=AD=6
∴△CQP∽△CMD CM=6
∴
∴
∴t=
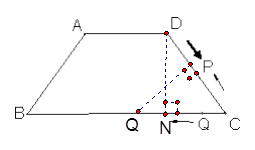
小题3:（3）如图，当∠PQC=90°时，易证
∴△CQP∽△CND
∴
∴
∴t=
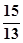
如图，当∠CPQ=90°时，易证
∴△CQP∽△CDN
∴
∴
∴t=
综上所述，当 t=或t=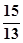 时点P、Q、C三点构成RT△略
练习册系列答案
名校课堂系列答案
相关题目
为
轴正半轴上一点，
两点关于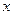
轴对称，过点
于
，
两点
=∠
；
=60º，试求所有满足条件的直线
的函数解析式.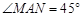 
，连结MC，NC，MN．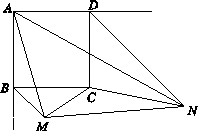
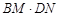= ；（用含a的代数式表示）
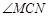的度数；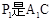
与AB的交点，点Q是
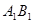与BC的交点，求证：
=
；
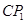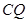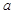,则CQ等于多少?
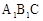绕点C顺时针旋转到△
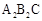（如图3），点
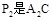与AP1的交点．当旋转角为多少度时,有△A P1C∽△CP1P2? 这时线段
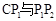之间存在一个怎样的数量关系?.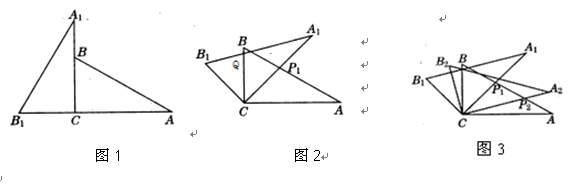
=
；③AC?BE=12；④3BF=4AC．其中结论正确的个数有（ ）
