题目内容
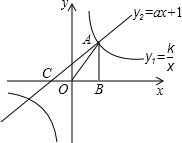
如图,已知反比例函数y=
(x>0)的图象与一次函数y=-
x+
的图象交于A、B两点,点C的坐标为(1,
),连接AC,AC平行于y轴.
(1)求反比例函数的解析式及点B的坐标;
(2)现有一个直角三角板,让它的直角顶点P在反比例函数图象上的A、B之间的部分滑动(不与A、B重合),两直角边始终分别平行于x轴、y轴,且与线段AB交于M、N两点,试判断P点在滑动过程中△PMN是否与△CAB总相似,简要说明判断理由.
| m |
| x |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
(1)求反比例函数的解析式及点B的坐标;
(2)现有一个直角三角板,让它的直角顶点P在反比例函数图象上的A、B之间的部分滑动(不与A、B重合),两直角边始终分别平行于x轴、y轴,且与线段AB交于M、N两点,试判断P点在滑动过程中△PMN是否与△CAB总相似,简要说明判断理由.

(1)由C(1,
)得A(1,2),代入反比例函数y=
中,得m=2,
∴反比例函数解析式为:y=
(x>0),(2分)
解方程组
,
由-
x+
=
化简得:x2-5x+4=0(x-4)(x-1)=0,
解得x1=4,x2=1,
∴B(4,
);(5分)
(2)无论P点在AB之间怎样滑动,△PMN与△CAB总能相似.
∵B、C两点纵坐标相等,∴BC∥x轴,
∵AC∥y轴,∴△CAB为直角三角形,
同时△PMN也是直角三角形,AC∥PM,BC∥PN,∴△PMN∽△CAB.(8分)
(在理由中只要能说出BC∥x轴,∠ACB=90°即可得分)
| 1 |
| 2 |
| m |
| x |
∴反比例函数解析式为:y=
| 2 |
| x |
解方程组
|
由-
| 1 |
| 2 |
| 5 |
| 2 |
| 2 |
| x |
解得x1=4,x2=1,
∴B(4,
| 1 |
| 2 |
(2)无论P点在AB之间怎样滑动,△PMN与△CAB总能相似.
∵B、C两点纵坐标相等,∴BC∥x轴,
∵AC∥y轴,∴△CAB为直角三角形,
同时△PMN也是直角三角形,AC∥PM,BC∥PN,∴△PMN∽△CAB.(8分)
(在理由中只要能说出BC∥x轴,∠ACB=90°即可得分)

练习册系列答案
相关题目

 标为4.
标为4.
 b(k>0)与x轴交于点A(a,0)、与y轴交于点B.
b(k>0)与x轴交于点A(a,0)、与y轴交于点B.